Advertisements
Advertisements
Question
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
Options
Domain = R+, Range = `(– oo, 1]`
Domain = R, Range = `(– oo, 2]`
Domain = R, Range = `(– oo, 2)`
Domain = R+, Range = `(– oo, 2]`
Solution
The domain and range of the function f given by f(x) = 2 – |x – 5| is Domain = R, Range = `(– oo, 2]`.
Explanation:
Given that: f(x) = 2 – |x – 5|
Here, f(x) is defined for x ∈ R
∴ Domain of f(x) = R
Now, x – 5 ≥ 0
⇒ – |x – 5| ≤ 0
⇒ 2 – |x – 5| ≤ 2
⇒ f(x) ≤ 2
∴ Range of f(x) = `(-oo, 2]`
APPEARS IN
RELATED QUESTIONS
If f(x) = x2, find `(f(1.1) - f(1))/((1.1 - 1))`
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(b) f2 = {(1, 1), (2, 7), (3, 5)}
If \[f\left( x \right) = \frac{x - 1}{x + 1}\] , then show that
(i) \[f\left( \frac{1}{x} \right) = - f\left( x \right)\]
(ii) \[f\left( - \frac{1}{x} \right) = - \frac{1}{f\left( x \right)}\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(i) f + g
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
If f(m) = m2 − 3m + 1, find f(0)
If f(m) = m2 − 3m + 1, find f(− x)
Find the domain and range of the following function.
f(x) = `sqrt(16 - x^2)`
Express the area A of a square as a function of its side s
Express the area A of circle as a function of its diameter d
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Express the following logarithmic equation in exponential form
ln 1 = 0
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Write the following expression as sum or difference of logarithm
In `(("a"^3 ("a" - 2)^2)/sqrt("b"^2 + 5))`
Prove that logbm a = `1/"m" log_"b""a"`
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Answer the following:
Let f: R → R be a function defined by f(x) = 5x3 – 8 for all x ∈ R, show that f is one-one and onto. Hence find f –1
Answer the following:
If f(x) = 3x4 – 5x2 + 7 find f(x – 1)
Answer the following:
If f(x) = 3x + a and f(1) = 7 find a and f(4)
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
Solve : `sqrt(log_2 x^4) + 4log_4 sqrt(2/x)` = 2
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
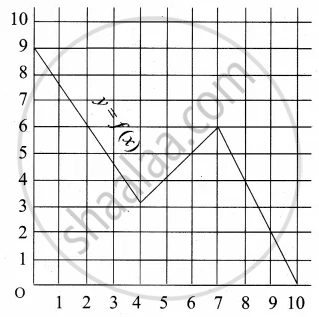
Describe the following Range
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
Range of the function f(x) = `x/(1 + x^2)` is ______.
