Advertisements
Advertisements
प्रश्न
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
पर्याय
Domain = R+, Range = `(– oo, 1]`
Domain = R, Range = `(– oo, 2]`
Domain = R, Range = `(– oo, 2)`
Domain = R+, Range = `(– oo, 2]`
उत्तर
The domain and range of the function f given by f(x) = 2 – |x – 5| is Domain = R, Range = `(– oo, 2]`.
Explanation:
Given that: f(x) = 2 – |x – 5|
Here, f(x) is defined for x ∈ R
∴ Domain of f(x) = R
Now, x – 5 ≥ 0
⇒ – |x – 5| ≤ 0
⇒ 2 – |x – 5| ≤ 2
⇒ f(x) ≤ 2
∴ Range of f(x) = `(-oo, 2]`
APPEARS IN
संबंधित प्रश्न
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, −4), (4, 2), (5, 1)} and g = {(1, 0), (2, 2), (3, −1), (4, 4), (5, 3)}
Find the domain of fg.
The range of f(x) = cos [x], for π/2 < x < π/2 is
If f(x) = sin [π2] x + sin [−π]2 x, where [x] denotes the greatest integer less than or equal to x, then
If f(x) = 3x + a and f(1) = 7 find a and f(4).
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Find the domain and range of the follwoing function.
h(x) = `sqrt(x + 5)/(5 + x)`
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x3
Express the following exponential equation in logarithmic form
e–x = 6
Select the correct answer from given alternatives.
If f : R → R is defined by f(x) = x3 then f–1 (8) is equal to :
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
Answer the following:
Find whether the following function is one-one
f : R − {3} → R defined by f(x) = `(5x + 7)/(x - 3)` for x ∈ R − {3}
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Answer the following:
Find the domain of the following function.
f(x) = x!
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
Given the function f: x → x2 – 5x + 6, evaluate f(2)
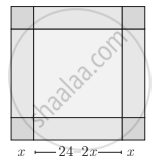
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
The domain of the function f(x) = log3+x (x2 - 1) is ______.
Domain of function f(x) = cos–1 6x is ______.
If f(x) = `1/sqrt(4 - 3x)`, then dom(f) = ______..
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Let f and g be two functions given by f = {(2, 4), (5, 6), (8, – 1), (10, – 3)} g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, – 5)} then. Domain of f + g is ______.
Find the domain of the following functions given by f(x) = x|x|
Domain of `sqrt(a^2 - x^2) (a > 0)` is ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
