Advertisements
Advertisements
प्रश्न
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
उत्तर
f(x) = `sqrtlog(x^2 - 6x + 6)`
is defined when
log(x2 − 6x + 6) ≥ 0
log(x2 − 6x + 6) ≥ 1 ⇒ (x - 5)(x - 1) ≥ 0
This inequality holds if x ≤ 1 or x ≥ 5. Hence, the domain of the function is (−∞, 1) ∪(5, ∞).
APPEARS IN
संबंधित प्रश्न
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(b) f2 = {(1, 1), (2, 7), (3, 5)}
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
If f(x) = x2, find \[\frac{f\left( 1 . 1 \right) - f\left( 1 \right)}{\left( 1 . 1 \right) - 1}\]
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
Write the domain and range of \[f\left( x \right) = \sqrt{x - \left[ x \right]}\] .
If f(x) = cos (log x), then the value of f(x2) f(y2) −
Let A = {x ∈ R : x ≠ 0, −4 ≤ x ≤ 4} and f : A ∈ R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\] for x ∈ A. Then th (is
If f(x) = sin [π2] x + sin [−π]2 x, where [x] denotes the greatest integer less than or equal to x, then
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
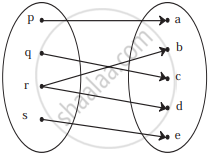
Check if the following relation is function:
If f(m) = m2 − 3m + 1, find f(− x)
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(0)
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Find the domain and range of the following function.
g(x) = `(x + 4)/(x - 2)`
Express the following exponential equation in logarithmic form
e2 = 7.3890
Write the following expression as a single logarithm.
5 log x + 7 log y − log z
Solve for x.
log2 + log(x + 3) – log(3x – 5) = log3
Solve for x.
2 log10 x = `1 + log_10 (x + 11/10)`
Select the correct answer from given alternatives.
If log10(log10(log10x)) = 0 then x =
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
Solve : `sqrt(log_2 x^4) + 4log_4 sqrt(2/x)` = 2
Answer the following:
If a2 = b3 = c4 = d5, show that loga bcd = `47/30`
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Answer the following:
Find the domain of the following function.
f(x) = 5–xPx–1
Given the function f: x → x2 – 5x + 6, evaluate f(– 1)
A graph representing the function f(x) is given in it is clear that f(9) = 2
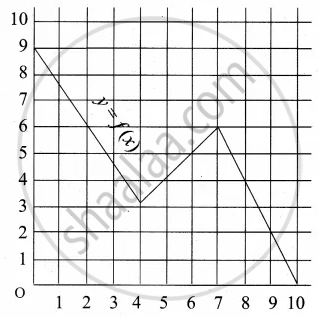
What is the image of 6 under f?
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Write an expression for gf(x) in its simplest form
Let A = {1, 2, 3, 4} and B = N. Let f : A → B be defined by f(x) = x3 then, find the range of f
Find the domain of the following function.
f(x) = [x] + x
Find the range of the following functions given by f(x) = 1 – |x – 2|
If f(x) = `(x - 1)/(x + 1)`, then show that `f(- 1/x) = (-1)/(f(x))`
Let f(x) and g(x) be two real polynomials of degree 2 and 1 respectively. If f(g(x)) = 8x2 – 2x, and g(f(x)) = 4x2 + 6x + 1, then the value of f(2) + g(2) is ______.
