Advertisements
Advertisements
प्रश्न
If f(x) = `(x - 1)/(x + 1)`, then show that `f(- 1/x) = (-1)/(f(x))`
उत्तर
f(x) = `(x - 1)/(x + 1)`
Substituting x by `– 1/x`, we get
`f(- 1/x) = ((- 1/x) - 1)/((- 1/ x) + 1)`
= `((-1 - x)/x)/((-1 + x)/x)`
= `(-1 - x)/(-1 + x)`
= `(-(x + 1))/(x - 1)`
= `(-1)/((x - 1)/(x + 1))`
Therefore,
`f(- 1/x) = (-1)/(f(x))`
Hence proved.
APPEARS IN
संबंधित प्रश्न
Define a function as a correspondence between two sets.
What is the fundamental difference between a relation and a function? Is every relation a function?
et A = (12, 13, 14, 15, 16, 17) and f : A → Z be a function given by
f(x) = highest prime factor of x.
Find range of f.
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
Write the range of the function f(x) = ex−[x], x ∈ R.
The range of f(x) = cos [x], for π/2 < x < π/2 is
Let f : R → R be defined by f(x) = 2x + |x|. Then f(2x) + f(−x) − f(x) =
The range of the function \[f\left( x \right) = \frac{x^2 - x}{x^2 + 2x}\] is
If \[f\left( x \right) = \frac{\sin^4 x + \cos^2 x}{\sin^2 x + \cos^4 x}\] for x ∈ R, then f (2002) =
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
Check if the relation given by the equation represents y as function of x:
3x − 6 = 21
lf f(x) = 3(4x+1), find f(– 3)
Given that log 2 = a and log 3 = b, write `log sqrt(96)` in terms of a and b
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
Answer the following:
Find the range of the following function.
f(x) = 1 + 2x + 4x
A graph representing the function f(x) is given in it is clear that f(9) = 2
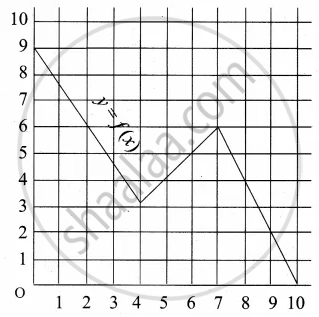
For what value of x is f(x) = 1?
A graph representing the function f(x) is given in it is clear that f(9) = 2
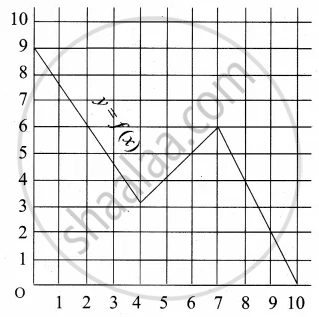
Describe the following Range
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
If f(x) = 5x - 3, then f-1(x) is ______
Domain of function f(x) = cos–1 6x is ______.
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Find the domain of the following functions given by f(x) = x|x|
Find the range of the following functions given by f(x) = 1 – |x – 2|
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
The value of the function f(x) = `(x^2 - 3x + 2)/(x^2 + x - 6)` lies in the interval
Let f(θ) = sin θ (sin θ + sin 3θ) then ______.
