Advertisements
Advertisements
प्रश्न
Answer the following:
Find the range of the following function.
f(x) = 1 + 2x + 4x
उत्तर
f(x) = 1 + 2x + 4x
Since, 2x > 0, 4x > 0
∴ f(x) > 1
∴ The range of function f = `(1, ∞)`
APPEARS IN
संबंधित प्रश्न
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
- {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
- {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
- {(1, 3), (1, 5), (2, 5)}
Define a function as a correspondence between two sets.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vii) f2 + 7f
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iv) \[\frac{g}{f}\] Also, find (f + g) (−1), (fg) (0),
If\[f\left( x \right) = 1 - \frac{1}{x}\] , then write the value of \[f\left( f\left( \frac{1}{x} \right) \right)\]
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
If \[\left[ x \right]^2 - 5\left[ x \right] + 6 = 0\], where [.] denotes the greatest integer function, then
If f(m) = m2 − 3m + 1, find f(− x)
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Let f be a subset of Z × Z defined by f = {(ab, a + b) : a, b ∈ Z}. Is f a function from Z to Z? Justify?
Express the following exponential equation in logarithmic form
e2 = 7.3890
Express the following logarithmic equation in exponential form
`log_(1/2) (8)` = – 3
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Solve for x.
log2 x + log4 x + log16 x = `21/4`
If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)2 = 20xy
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Select the correct answer from given alternatives.
If log10(log10(log10x)) = 0 then x =
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(0, 0), (1, 1), (1, –1), (4, 2), (4, –2), (9, 3), (9, –3), (16, 4), (16, –4)}
Answer the following:
Show that, `log ("a"^2/"bc") + log ("b"^2/"ca") + log ("c"^2/"ab")` = 0
Answer the following:
Find the range of the following function.
f(x) = `1/(1 + sqrt(x))`
Given the function f: x → x2 – 5x + 6, evaluate f(2)
A graph representing the function f(x) is given in it is clear that f(9) = 2
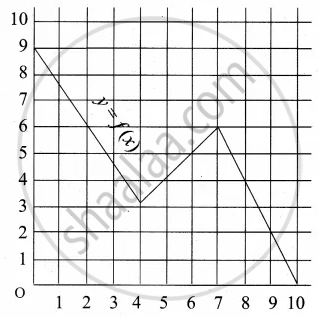
What is the image of 6 under f?
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
If f(x) = `{{:(x^2",", x ≥ 0),(x^3",", x < 0):}`, then f(x) is ______.
Redefine the function f(x) = x − 2 + 2 + x , – 3 ≤ x ≤ 3
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f – g)(x)
Let f(x) = `sqrt(1 + x^2)`, then ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
If f : R – {2} `rightarrow` R i s a function defined by f(x) = `(x^2 - 4)/(x - 2)`, then its range is ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
