Advertisements
Advertisements
प्रश्न
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
उत्तर
It is given that A and B are two sets such that n(A) = p and n(B) = q.
Now, any element of set A, say ai (1 ≤ i ≤ p), is related with an element of set B in q ways. Similarly, other elements of set A are related with an element of set B in q ways.
Thus, every element of set A is related with every element of set B in q ways.
∴ Total number of functions from A to B = q × q × q × ... × q (p times) = qp
APPEARS IN
संबंधित प्रश्न
What is the fundamental difference between a relation and a function? Is every relation a function?
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(b) {x : f(x) = −2}
f, g, h are three function defined from R to R as follow:
(iii) h(x) = x2 + 1
Find the range of function.
et A = (12, 13, 14, 15, 16, 17) and f : A → Z be a function given by
f(x) = highest prime factor of x.
Find range of f.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
If f(x) = 4x − x2, x ∈ R, then write the value of f(a + 1) −f(a − 1).
If f, g, h are real functions given by f(x) = x2, g(x) = tan x and h(x) = loge x, then write the value of (hogof)\[\left( \sqrt{\frac{\pi}{4}} \right)\] .
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
Find the set of values of x for which the functions f(x) = 3x2 − 1 and g(x) = 3 + x are equal.
If f(x) = cos (log x), then value of \[f\left( x \right) f\left( 4 \right) - \frac{1}{2} \left\{ f\left( \frac{x}{4} \right) + f\left( 4x \right) \right\}\] is
The domain of the function \[f\left( x \right) = \sqrt{\frac{\left( x + 1 \right) \left( x - 3 \right)}{x - 2}}\] is
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
The range of the function f(x) = |x − 1| is
Check if the following relation is function:

If f(m) = m2 − 3m + 1, find f(−3)
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Express the area A of circle as a function of its radius r
Express the following exponential equation in logarithmic form
231 = 23
Express the following logarithmic equation in exponential form
log2 64 = 6
Express the following logarithmic equation in exponential form
`log_(1/2) (8)` = – 3
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f + g) (x)
Select the correct answer from given alternatives.
If log (5x – 9) – log (x + 3) = log 2 then x = ...............
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Given the function f: x → x2 – 5x + 6, evaluate f(2)
A graph representing the function f(x) is given in it is clear that f(9) = 2
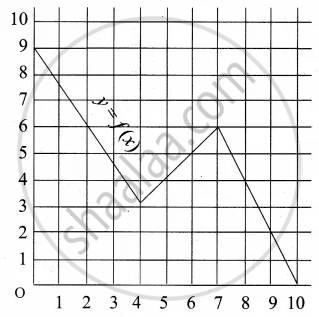
Describe the following Domain
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
If f(x) = `(x - 1)/(x + 1), x ≠ - 1` Show that f(f(x)) = `- 1/x`, Provided x ≠ 0
Find the domain of the following functions given by f(x) = x|x|
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
The expression \[\begin{array}{cc}\log_p\log_p\sqrt[p]{\sqrt[p]{\sqrt[p]{\text{...........}\sqrt[p]{p}}}}\\
\phantom{...........}\ce{\underset{n radical signs}{\underline{\uparrow\phantom{........}\uparrow}}}
\end{array}\]where p ≥ 2, p ∈ N; ∈ N when simplified is ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
The range of the function f(x) = x2 + 2x+ 2 is ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
