Advertisements
Advertisements
प्रश्न
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
उत्तर
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
= `2"In"[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]`
= `2{"In" [root(3)(x - 2)(2x + 1)^4] - "In"[(x + 4)sqrt(2x + 4)]}`
= `2{"In"(x - 2)^(1/3) + "In" (2x + 1)^4 - ["In"(x + 4) + "In"(2x + 4)^(1/2)]}`
= `2{1/3 "In"(x - 2) + 4"In"(2x + 1) - "In"(x + 4) - 1/2"In"(2x + 4)}`
APPEARS IN
संबंधित प्रश्न
Define a function as a correspondence between two sets.
f, g, h are three function defined from R to R as follow:
(i) f(x) = x2
Find the range of function.
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
Let A = [p, q, r, s] and B = [1, 2, 3]. Which of the following relations from A to B is not a function?
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vii) f2 + 7f
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
f is a real valued function given by \[f\left( x \right) = 27 x^3 + \frac{1}{x^3}\] and α, β are roots of \[3x + \frac{1}{x} = 12\] . Then,
The domain of definition of the function f(x) = log |x| is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
Check if the following relation is function:

If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(3)
Check if the following relation is a function.
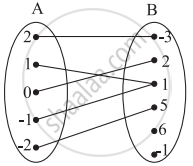
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
Check if the relation given by the equation represents y as function of x:
x + y2 = 9
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Express the following logarithmic equation in exponential form
ln 1 = 0
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Select the correct answer from given alternatives.
If log10(log10(log10x)) = 0 then x =
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Answer the following:
If f(x) = 3x + a and f(1) = 7 find a and f(4)
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
Find value of `(3 + log_10 343)/(2 + 1/2 log_10 (49/4) + 1/2 log_10 (1/25)`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
Answer the following:
Find the range of the following function.
f(x) = 1 + 2x + 4x
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
If f(x) = 5x - 3, then f-1(x) is ______
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
Find the domain of the following function given by:
f(x) = `(3x)/(2x - 8)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
If f(x) = y = `(ax - b)/(cx - a)`, then prove that f(y) = x.
Domain of `sqrt(a^2 - x^2) (a > 0)` is ______.
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
If f(x) = x3 – 1 and domain of f = {0, 1, 2, 3}, then domain of f–1 is ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
If f : R – {2} `rightarrow` R i s a function defined by f(x) = `(x^2 - 4)/(x - 2)`, then its range is ______.
