Advertisements
Advertisements
प्रश्न
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
उत्तर
If f : A → B is such that y ∈ B, then \[f^{- 1}\] { y }={x ∈ A: f (x) = y}.
In other words, f -1{ y} is the set of pre - images of y.
Let
Then, f (x) =17 .
⇒ x2 +1 = 17
⇒ x2 = 17 -1 = 16
⇒ x = ± 4
∴ \[f^{- 1}\] {17} = { -4,4}
Then, f (x) =-3
⇒ x2 + 1 = -3
⇒ x2 =- 3 - 1 = -4
So
APPEARS IN
संबंधित प्रश्न
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
If \[f\left( x \right) = x^3 - \frac{1}{x^3}\] , show that
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(ii) g − f
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] . Then write the value of α satisfying f(f(x)) = x for all x ≠ −1.
Find the set of values of x for which the functions f(x) = 3x2 − 1 and g(x) = 3 + x are equal.
If f : Q → Q is defined as f(x) = x2, then f−1 (9) is equal to
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right) \text{ and} g\left( x \right) = \frac{3x + x^3}{1 + 3 x^2}\] , then f(g(x)) is equal to
If \[f\left( x \right) = \frac{\sin^4 x + \cos^2 x}{\sin^2 x + \cos^4 x}\] for x ∈ R, then f (2002) =
Check if the following relation is function:
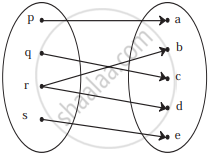
If f(m) = m2 − 3m + 1, find f(−3)
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Check if the following relation is a function.
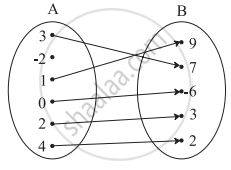
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
Find x, if f(x) = g(x) where f(x) = x4 + 2x2, g(x) = 11x2
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Express the following exponential equation in logarithmic form
`9^(3/2)` = 27
Express the following logarithmic equation in exponential form
ln e = 1
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
Write the following expression as a single logarithm.
ln (x + 2) + ln (x − 2) − 3 ln (x + 5)
Prove that alogcb = blogca
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f + g) (x)
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Answer the following:
Find the domain of the following function.
f(x) = x!
A function f is defined by f(x) = 2x – 3 find `("f"(0) + "f"(1))/2`
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
If f(x) = `{{:(x^2",", x ≥ 0),(x^3",", x < 0):}`, then f(x) is ______.
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
Range of f(x) = `1/(1 - 2 cosx)` is ______.
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
If f : R – {2} `rightarrow` R i s a function defined by f(x) = `(x^2 - 4)/(x - 2)`, then its range is ______.
