Advertisements
Advertisements
Question
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
Solution
It is given that A and B are two sets such that n(A) = p and n(B) = q.
Now, any element of set A, say ai (1 ≤ i ≤ p), is related with an element of set B in q ways. Similarly, other elements of set A are related with an element of set B in q ways.
Thus, every element of set A is related with every element of set B in q ways.
∴ Total number of functions from A to B = q × q × q × ... × q (p times) = qp
APPEARS IN
RELATED QUESTIONS
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(b) pre-images of 6, −3 and 5.
Let f : R → R and g : C → C be two functions defined as f(x) = x2 and g(x) = x2. Are they equal functions?
f, g, h are three function defined from R to R as follow:
(iii) h(x) = x2 + 1
Find the range of function.
If \[f\left( x \right) = \frac{2x}{1 + x^2}\] , show that f(tan θ) = sin 2θ.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iii) \[\frac{f}{g}\]
Write the domain and range of \[f\left( x \right) = \sqrt{x - \left[ x \right]}\] .
Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, −4), (4, 2), (5, 1)} and g = {(1, 0), (2, 2), (3, −1), (4, 4), (5, 3)}
Find the domain of fg.
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
The domain of definition of the function f(x) = log |x| is
Let \[f\left( x \right) = \sqrt{x^2 + 1}\ ] . Then, which of the following is correct?
Check if the following relation is function:

If f(m) = m2 − 3m + 1, find f(0)
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Check if the following relation is a function.
Check if the relation given by the equation represents y as function of x:
2x + 3y = 12
If f(m) = m2 − 3m + 1, find f(x + 1)
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
lf f(x) = 3(4x+1), find f(– 3)
Solve for x.
2 log10 x = `1 + log_10 (x + 11/10)`
If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)2 = 20xy
The equation logx2 16 + log2x 64 = 3 has,
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
A graph representing the function f(x) is given in it is clear that f(9) = 2
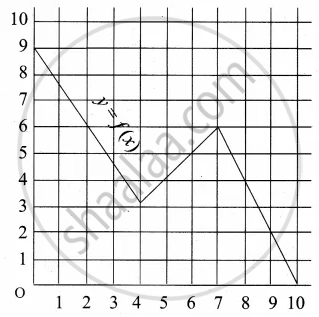
For what value of x is f(x) = 1?
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Write an expression for gf(x) in its simplest form
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
If f(x) = `{{:(x^2",", x ≥ 0),(x^3",", x < 0):}`, then f(x) is ______.
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Find the domain of the following functions given by f(x) = `1/sqrt(1 - cos x)`
Find the domain of the following functions given by f(x) = x|x|
Domain of `sqrt(a^2 - x^2) (a > 0)` is ______.
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
