Advertisements
Advertisements
Question
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
Solution
Given:
\[f\left( x \right) = \sqrt{x + 1}\text{ and } g\left( x \right) = \sqrt{9 - x^2}\]
Clearly,
Thus, domain (f) = [1, ∞]
Again,
⇒ \[x \in \left[ - 3, 3 \right]\]
APPEARS IN
RELATED QUESTIONS
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(ii) g − f
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(v) \[\frac{g}{f}\]
Let f(x) = x2 and g(x) = 2x+ 1 be two real functions. Find (f + g) (x), (f − g) (x), (fg) (x) and \[\left( \frac{f}{g} \right) \left( x \right)\] .
Which one of the following is not a function?
If \[3f\left( x \right) + 5f\left( \frac{1}{x} \right) = \frac{1}{x} - 3\] for all non-zero x, then f(x) =
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
The domain of the function \[f\left( x \right) = \sqrt{\frac{\left( x + 1 \right) \left( x - 3 \right)}{x - 2}}\] is
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
If \[\left[ x \right]^2 - 5\left[ x \right] + 6 = 0\], where [.] denotes the greatest integer function, then
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
Check if the following relation is a function.
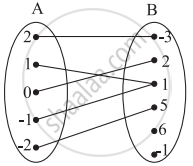
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
If f(m) = m2 − 3m + 1, find f(−3)
Find the domain and range of the following function.
g(x) = `(x + 4)/(x - 2)`
Express the area A of a square as a function of its side s
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Check the injectivity and surjectivity of the following function.
f : R → R given by f(x) = x3
Write the following expression as a single logarithm.
`1/3 log (x - 1) + 1/2 log (x)`
Prove that alogcb = blogca
Select the correct answer from given alternatives.
If log (5x – 9) – log (x + 3) = log 2 then x = ...............
Select the correct answer from given alternatives.
If f : R → R is defined by f(x) = x3 then f–1 (8) is equal to :
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(0, 0), (1, 1), (1, –1), (4, 2), (4, –2), (9, 3), (9, –3), (16, 4), (16, –4)}
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range
{(12, 1), (3, 1), (5, 2)}
Answer the following:
A function f is defined as f(x) = 4x + 5, for – 4 ≤ x < 0. Find the values of f(–1), f(–2), f(0), if they exist
Answer the following:
Let f : R → R be given by f(x) = x + 5 for all x ∈ R. Draw its graph
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
Given the function f: x → x2 – 5x + 6, evaluate f(2)
A graph representing the function f(x) is given in it is clear that f(9) = 2
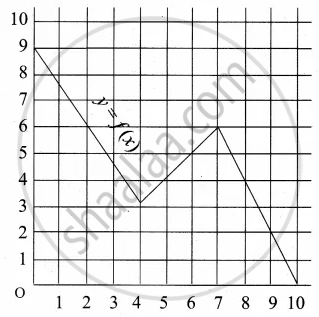
What is the image of 6 under f?
If the domain of function f(a) = a2 - 4a + 8 is (-∞, ∞), then the range of function is ______
The domain of the real valued function f(x) = `sqrt((x - 2)/(3 - x))` is ______.
Let f : R → R be defined by
f(x) = `{(3x; x > 2),(2x^2; 1 ≤ x ≤ 2), (4x; x < 1):}`
Then f(-2) + f(1) + f(3) is ______
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
The value of the function f(x) = `(x^2 - 3x + 2)/(x^2 + x - 6)` lies in the interval
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
