Advertisements
Advertisements
Question
Which one of the following is not a function?
Options
(a) {(x, y) : x, y ∈ R, x2 = y}
(b) {(x, y) : x, y ∈, R, y2 = x}
(c) {(x, y) : x, y ∈ R, x2 = y3}
(d) {(x, y) : x, y ∈, R, y = x3}
Solution
(b) {(x, y) : x, y ∈, R, y2 = x}
\[y^2 = x \text{ gives two values of y for a value of x }. \]
\[i . e .\text{ there are two images for a value of x } . \]
\[\text{ For example: } (2 )^2 = 4 \text{ and } ( - 2 )^2 = 4\]
\[\text{ Thus, it is not a function . } \]
APPEARS IN
RELATED QUESTIONS
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
Let A = {x ∈ R : x ≠ 0, −4 ≤ x ≤ 4} and f : A ∈ R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\] for x ∈ A. Then th (is
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
If f(x) = 3x + a and f(1) = 7 find a and f(4).
Check if the following relation is a function.
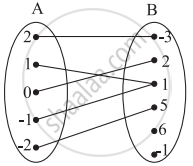
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
Check if the relation given by the equation represents y as function of x:
x + y2 = 9
Find x, if f(x) = g(x) where f(x) = x4 + 2x2, g(x) = 11x2
Find the domain and range of the following function.
f(x) = `sqrt((x - 3)/(7 - x))`
Express the area A of a square as a function of its perimeter P
lf f(x) = 3(4x+1), find f(– 3)
Express the following exponential equation in logarithmic form
25 = 32
Express the following exponential equation in logarithmic form
231 = 23
Find the domain of f(x) = ln (x − 5)
Find the domain of f(x) = log10 (x2 − 5x + 6)
Solve for x.
log2 x + log4 x + log16 x = `21/4`
Select the correct answer from given alternative.
The domain and range of f(x) = 2 − |x − 5| is
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(0, 0), (1, 1), (1, –1), (4, 2), (4, –2), (9, 3), (9, –3), (16, 4), (16, –4)}
Answer the following:
A function f is defined as f(x) = 4x + 5, for – 4 ≤ x < 0. Find the values of f(–1), f(–2), f(0), if they exist
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
Given the function f: x → x2 – 5x + 6, evaluate f(2)
A graph representing the function f(x) is given in it is clear that f(9) = 2
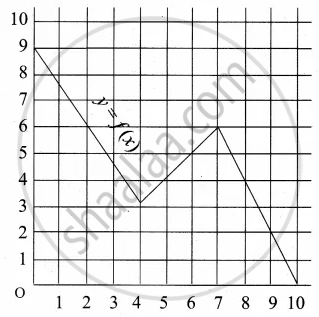
What is the image of 6 under f?
A function f is defined by f(x) = 2x – 3 find `("f"(0) + "f"(1))/2`
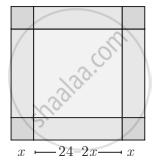
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
Redefine the function which is given by f(x) = `|x - 1| + |1 + x|, -2 ≤ x ≤ 2`
Find the domain of the function f given by f(x) = `1/sqrt([x]^2 - [x] - 6)`
Find the domain of the following functions given by f(x) = `1/sqrt(1 - cos x)`
Find the range of the following functions given by f(x) = |x − 3|
Domain of `sqrt(a^2 - x^2) (a > 0)` is ______.
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
