A function f is defined by f(x) = 2x – 3 find f(0)+f(1)2 - Mathematics

A function f is defined by f(x) = 2x – 3 find `("f"(0) + "f"(1))/2`

Sum

f(x) = 2x – 3

f(0) = 2(0) – 3 = – 3

f(1) = 2(1) – 3 = 2 – 3 = – 1

`("f"(0) + "f"(1))/2= (-3 - 1)/2 = (-4)/2`

`("f"(0) + "f"(1))/2` = – 2

shaalaa.com

Is there an error in this question or solution?

Chapter 1: Relations and Functions - Exercise 1.3 [Page 14]

Chapter 1 Relations and Functions
Exercise 1.3 | Q 6. (i) | Page 14

If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =

The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is

Check if the following relation is function:

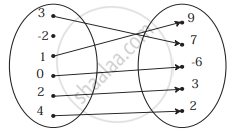
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.

{(1, 1), (2, 1), (3, 1), (4, 1)}

Find x, if g(x) = 0 where g(x) = x³− 2x² − 5x + 6

Express the following exponential equation in logarithmic form

`"e"^(1/2)` = 1.6487

If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)² = 20xy

Answer the following:

For any base show that log (1 + 2 + 3) = log 1 + log 2 + log 3

Find the range of the following functions given by `sqrt(16 - x^2)`

Redefine the function f(x) = x − 2 + 2 + x , – 3 ≤ x ≤ 3