Advertisements
Advertisements
Question
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
Solution
f(x) = 2x + 5
f(x + 2) = 2(x + 2) + 5
= 2x + 4 + 5
= 2x + 9
f(2) = (2) + 5
= 4 + 5
= 9
`(f(x + 2) -"f"(2))/x = (2x + 9 - 9)/x`
= `(2x)/x`
= 2
`(f(x + 2) -"f"(2))/x = 2`
APPEARS IN
RELATED QUESTIONS
If \[f\left( x \right) = \frac{2x}{1 + x^2}\] , show that f(tan θ) = sin 2θ.
If A = {1, 2, 3} and B = {x, y}, then the number of functions that can be defined from A into B is
The domain of the function \[f\left( x \right) = \sqrt{\frac{\left( x + 1 \right) \left( x - 3 \right)}{x - 2}}\] is
Check if the following relation is function:
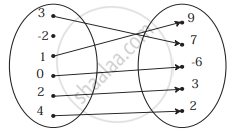
Check if the relation given by the equation represents y as function of x:
x + y2 = 9
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Express the following exponential equation in logarithmic form
`9^(3/2)` = 27
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
A graph representing the function f(x) is given in it is clear that f(9) = 2
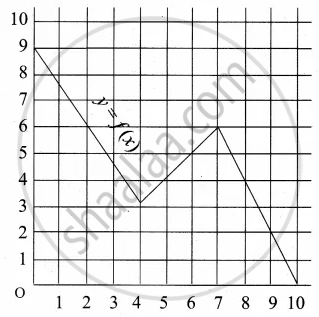
What is the image of 6 under f?
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
