Advertisements
Advertisements
Question
A graph representing the function f(x) is given in it is clear that f(9) = 2
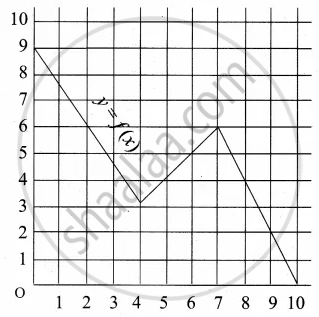
What is the image of 6 under f?
Solution
The image of 6 under f is 5.
APPEARS IN
RELATED QUESTIONS
Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(c) f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
If f : Q → Q is defined as f(x) = x2, then f−1 (9) is equal to
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
Check if the following relation is function:
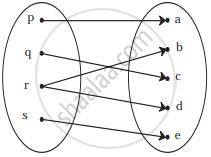
Check if the following relation is a function.
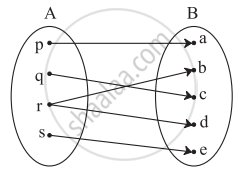
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
A function f is defined by f(x) = 2x – 3 find x such that f(x) = f(1 – x)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
