Advertisements
Advertisements
Question
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
Solution
Given:
\[f\left( x \right) = \sqrt{x + 1}\text{ and } g\left( x \right) = \sqrt{9 - x^2}\]
Clearly,
Thus, domain (f) = [1, ∞]
Again,
⇒ \[x \in \left[ - 3, 3 \right]\]
APPEARS IN
RELATED QUESTIONS
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.
What is the fundamental difference between a relation and a function? Is every relation a function?
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
If \[y = f\left( x \right) = \frac{ax - b}{bx - a}\] , show that x = f(y).
If f(x) = (a − xn)1/n, a > 0 and n ∈ N, then prove that f(f(x)) = x for all x.
If for non-zero x, af(x) + bf \[\left( \frac{1}{x} \right) = \frac{1}{x} - 5\] , where a ≠ b, then find f(x).
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iii) \[\frac{f}{g}\]
The range of the function \[f\left( x \right) = \frac{x^2 - x}{x^2 + 2x}\] is
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
Check if the following relation is function:
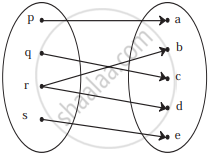
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
If f(m) = m2 − 3m + 1, find f(0)
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
Find the domain and range of the following function.
f(x) = `sqrt(16 - x^2)`
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Given that log 2 = a and log 3 = b, write `log sqrt(96)` in terms of a and b
Select the correct answer from given alternatives.
Find x, if 2log2 x = 4
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
If f(x) = `{{:(x^2",", x ≥ 0),(x^3",", x < 0):}`, then f(x) is ______.
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Find the range of the following functions given by `sqrt(16 - x^2)`
Find the domain of the function f given by f(x) = `1/sqrt([x]^2 - [x] - 6)`
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
If f(x) = `x^3 - 1/x^3`, then `f(x) + f(1/x)` is equal to ______.
Redefine the function f(x) = x − 2 + 2 + x , – 3 ≤ x ≤ 3
Range of f(x) = `1/(1 - 2 cosx)` is ______.
Domain of `sqrt(a^2 - x^2) (a > 0)` is ______.
The domain and range of the real function f defined by f(x) = `(4 - x)/(x - 4)` is given by ______.
The domain of the function f given by f(x) = `(x^2 + 2x + 1)/(x^2 - x - 6)` is ______.
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
