Advertisements
Advertisements
Question
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Solution
For f(x) = g(x)
⇒ 2x2 – 1 = 1 – 3x
⇒ 2x2 + 3x – 2 = 0
⇒ 2x2 + 4x – x – 2 = 0
⇒ 2x(x + 2) – 1(x + 2) = 0
⇒ (2x – 1)(x + 2) = 0
Thus domain for which the function f(x) = g(x) is `{1/2, -2}`.
APPEARS IN
RELATED QUESTIONS
If f(x) = x2, find `(f(1.1) - f(1))/((1.1 - 1))`
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
The domain of the function
If \[\left[ x \right]^2 - 5\left[ x \right] + 6 = 0\], where [.] denotes the greatest integer function, then
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
Check if the following relation is a function.
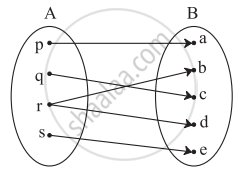
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 3), (4, 1), (2, 2)}
Find x, if g(x) = 0 where g(x) = `(18 -2x^2)/7`
Find the domain and range of the following function.
f(x) = `root(3)(x + 1)`
Express the following logarithmic equation in exponential form
`log_5 1/25` = – 2
If f(x) = 3x + 5, g(x) = 6x − 1, then find `("f"/"g") (x)` and its domain
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
Answer the following:
Show that, `log |sqrt(x^2 + 1) + x | + log | sqrt(x^2 + 1) - x|` = 0
Answer the following:
Show that, `log ("a"^2/"bc") + log ("b"^2/"ca") + log ("c"^2/"ab")` = 0
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
Solve : `sqrt(log_2 x^4) + 4log_4 sqrt(2/x)` = 2
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
Answer the following:
Find the range of the following function.
f(x) = 1 + 2x + 4x
A function f is defined by f(x) = 2x – 3 find x such that f(x) = 0
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
Find the domain of the following function.
f(x) = [x] + x
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
The range of the function y = `1/(2 - sin3x)` is ______.
The expression \[\begin{array}{cc}\log_p\log_p\sqrt[p]{\sqrt[p]{\sqrt[p]{\text{...........}\sqrt[p]{p}}}}\\
\phantom{...........}\ce{\underset{n radical signs}{\underline{\uparrow\phantom{........}\uparrow}}}
\end{array}\]where p ≥ 2, p ∈ N; ∈ N when simplified is ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
Range of the function f(x) = `x/(1 + x^2)` is ______.
