Advertisements
Advertisements
Question
Express the following logarithmic equation in exponential form
`log_5 1/25` = – 2
Solution
`log_5 1/25` = – 2
∴ `1/25` = 5–2 i.e. 5–2 = `1/25`
APPEARS IN
RELATED QUESTIONS
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iv) \[\frac{g}{f}\] Also, find (f + g) (−1), (fg) (0),
If f, g, h are real functions given by f(x) = x2, g(x) = tan x and h(x) = loge x, then write the value of (hogof)\[\left( \sqrt{\frac{\pi}{4}} \right)\] .
The range of f(x) = cos [x], for π/2 < x < π/2 is
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
If \[3f\left( x \right) + 5f\left( \frac{1}{x} \right) = \frac{1}{x} - 3\] for all non-zero x, then f(x) =
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The range of the function f(x) = |x − 1| is
Which of the following relations are functions? If it is a function determine its domain and range:
{(1, 1), (3, 1), (5, 2)}
Check if the following relation is a function.
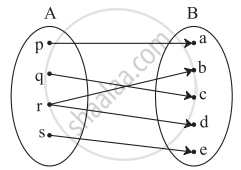
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 1), (2, 1), (3, 1), (4, 1)}
If f(m) = m2 − 3m + 1, find `f(1/2)`
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
Find x, if g(x) = 0 where g(x) = x3 − 2x2 − 5x + 6
Find the domain and range of the following function.
g(x) = `(x + 4)/(x - 2)`
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Express the following exponential equation in logarithmic form
54° = 1
Express the following exponential equation in logarithmic form
`"e"^(1/2)` = 1.6487
Find the domain of f(x) = log10 (x2 − 5x + 6)
Prove that logbm a = `1/"m" log_"b""a"`
Solve for x.
log2 + log(x + 3) – log(3x – 5) = log3
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
If f(x) = log(1 – x), 0 ≤ x < 1 show that `"f"(1/(1 + x))` = f(1 – x) – f(– x)
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find the length of forehand of a person if the height is 53.3 inches
Let A = {1, 2, 3, 4} and B = N. Let f : A → B be defined by f(x) = x3 then, find the range of f
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
Let f and g be two functions given by f = {(2, 4), (5, 6), (8, – 1), (10, – 3)} g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, – 5)} then. Domain of f + g is ______.
Redefine the function f(x) = x − 2 + 2 + x , – 3 ≤ x ≤ 3
The range of the function y = `1/(2 - sin3x)` is ______.
The range of the function f(x) = x2 + 2x+ 2 is ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
The period of the function
f(x) = `(sin 8x cos x - sin 6x cos 3x)/(cos 2x cos x - sin 3x sin 4x)` is ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
