Advertisements
Advertisements
Question
If \[3f\left( x \right) + 5f\left( \frac{1}{x} \right) = \frac{1}{x} - 3\] for all non-zero x, then f(x) =
Options
(a) \[\frac{1}{14}\left( \frac{3}{x} + 5x - 6 \right)\]
(b) \[\frac{1}{14}\left( - \frac{3}{x} + 5x - 6 \right)\]
(c) \[\frac{1}{14}\left( - \frac{3}{x} + 5x + 6 \right)\]
(d) None of these
Solution
(d) None of these
\[3f\left( x \right) + 5f\left( \frac{1}{x} \right) = \frac{1}{x} - 3\]
\[\text{ Multiplying (1) by } 3: \]
\[15 f\left( \frac{1}{x} \right) + 9 f(x) = \frac{3}{x} - 9 . . . . . (2)\]
\[\text{ Replacing x by} \frac{1}{x}\text{ in } (1): \]
\[3 f\left( \frac{1}{x} \right) + 5 f(x) = x - 3 \]
\[\text{ Multiplying by } 5: \]
\[15 f\left( \frac{1}{x} \right) + 25 f(x) = 5x - 15 . . . . (3)\]
\[\text{ Solving (2) and (3) } : \]
\[ - 16 f(x) = \frac{3}{x} - 5x + 6\]
\[ \Rightarrow f(x) = \frac{1}{16}\left( - \frac{3}{x} + 5x - 6 \right)\]
Notes
Disclaimer: The question in the book has some error, so, none of the options are matching with the solution. The solution is created according to the question given in the book.
APPEARS IN
RELATED QUESTIONS
If f(x) = x2, find `(f(1.1) - f(1))/((1.1 - 1))`
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If \[f\left( x \right) = \frac{2x}{1 + x^2}\] , show that f(tan θ) = sin 2θ.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
If f, g and h are real functions defined by
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
Which of the following are functions?
The domain of definition of the function f(x) = log |x| is
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Check if the following relation is a function.
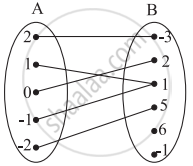
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Let f be a subset of Z × Z defined by f = {(ab, a + b) : a, b ∈ Z}. Is f a function from Z to Z? Justify?
Check the injectivity and surjectivity of the following function.
f : R → R given by f(x) = x3
Express the following exponential equation in logarithmic form
231 = 23
Express the following exponential equation in logarithmic form
`9^(3/2)` = 27
Express the following exponential equation in logarithmic form
e–x = 6
Express the following logarithmic equation in exponential form
ln e = 1
Prove that logbm a = `1/"m" log_"b""a"`
If f(x) = ax2 − bx + 6 and f(2) = 3 and f(4) = 30, find a and b
Solve for x.
log2 + log(x + 3) – log(3x – 5) = log3
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
Show that `7log (15/16) + 6log(8/3) + 5log (2/5) + log(32/25)` = log 3
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
Answer the following:
Find the domain of the following function.
f(x) = 5–xPx–1
Answer the following:
Find the range of the following function.
f(x) = [x] – x
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
A graph representing the function f(x) is given in it is clear that f(9) = 2
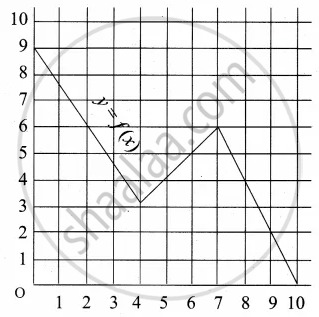
For what value of x is f(x) = 1?
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
Let A and B be any two sets such that n(B) = p, n(A) = q then the total number of functions f : A → B is equal to ______.
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Find the domain of the following function given by:
f(x) = `(3x)/(2x - 8)`
Which of the following functions is NOT one-one?
If f : R – {2} `rightarrow` R i s a function defined by f(x) = `(x^2 - 4)/(x - 2)`, then its range is ______.
The range of the function f(x) = `""^(7 - x)P_(x - 3)` is ______.
