Advertisements
Advertisements
Question
The domain of definition of the function f(x) = log |x| is
Options
(a) R
(b) (−∞, 0)
(c) (0, ∞)
(d) R − {0}
Solution
(d) R − {0}
f(x) = log |x|
\[\text{ For f(x) to be defined,} \]
\[\left| x \right| > 0, \text{ which is always true . } \]
\[\text{ But } \left| x \right| \neq 0\]
\[ \Rightarrow x \neq 0\]
\[\text{ Thus, dom }(f) = R - {0} . \]
APPEARS IN
RELATED QUESTIONS
Define a function as a correspondence between two sets.
find: f(1), f(−1), f(0) and f(2).
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If \[f\left( x \right) = \frac{x + 1}{x - 1}\] , show that f[f[(x)]] = x.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(ii) g − f
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] . Then write the value of α satisfying f(f(x)) = x for all x ≠ −1.
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
If f(x) = 4x − x2, x ∈ R, then write the value of f(a + 1) −f(a − 1).
Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, −4), (4, 2), (5, 1)} and g = {(1, 0), (2, 2), (3, −1), (4, 4), (5, 3)}
Find the domain of fg.
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Express the following exponential equation in logarithmic form
25 = 32
Express the following logarithmic equation in exponential form
log10 (0.001) = −3
Write the following expression as sum or difference of logarithm
In `(("a"^3 ("a" - 2)^2)/sqrt("b"^2 + 5))`
Prove that alogcb = blogca
The equation logx2 16 + log2x 64 = 3 has,
Answer the following:
Let f : R – {2} → R be defined by f(x) = `(x^2 - 4)/(x - 2)` and g : R → R be defined by g(x) = x + 2. Examine whether f = g or not
Answer the following:
For any base show that log (1 + 2 + 3) = log 1 + log 2 + log 3
Answer the following:
Show that `7log (15/16) + 6log(8/3) + 5log (2/5) + log(32/25)` = log 3
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
A graph representing the function f(x) is given in it is clear that f(9) = 2
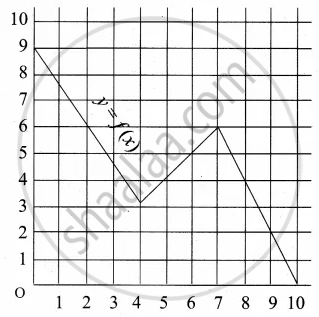
What is the image of 6 under f?
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
The range of the function f(x) = `(x^2 - 3x + 2)/(x^3 - 4x^2 + 5x - 2)` is ______
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
If f(x) = `1/sqrt(4 - 3x)`, then dom(f) = ______..
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Redefine the function which is given by f(x) = `|x - 1| + |1 + x|, -2 ≤ x ≤ 2`
Let A and B be any two sets such that n(B) = p, n(A) = q then the total number of functions f : A → B is equal to ______.
Find the domain of the following functions given by f(x) = x|x|
Find the range of the following functions given by f(x) = |x − 3|
If f(x) = `(x - 1)/(x + 1)`, then show that `f(- 1/x) = (-1)/(f(x))`
If f(x) = y = `(ax - b)/(cx - a)`, then prove that f(y) = x.
The domain and range of the real function f defined by f(x) = `(4 - x)/(x - 4)` is given by ______.
The domain of the function f given by f(x) = `(x^2 + 2x + 1)/(x^2 - x - 6)` is ______.
The expression \[\begin{array}{cc}\log_p\log_p\sqrt[p]{\sqrt[p]{\sqrt[p]{\text{...........}\sqrt[p]{p}}}}\\
\phantom{...........}\ce{\underset{n radical signs}{\underline{\uparrow\phantom{........}\uparrow}}}
\end{array}\]where p ≥ 2, p ∈ N; ∈ N when simplified is ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
