Advertisements
Advertisements
Question
Define a function as a correspondence between two sets.
Solution
A function is a correspondence between two sets of elements, such that for each element in the first set there is only one corresponding element in the second set.
The first set is called the domain and the set of all corresponding elements in the second set is called the range.
Let A = {1, 2, 3} and B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Let f : A → B be the correspondence which assigns to each element in A its square.
Hence,
f (1) = 12 = 1
f (2) = 22 = 4
f (3) = 32 = 9
Since for each element (1 or 2 or 3) of A, there is exactly one element of B, so f is a function.
In this case, every element of B is not an image of some element of A.
APPEARS IN
RELATED QUESTIONS
Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.
f, g, h are three function defined from R to R as follow:
(i) f(x) = x2
Find the range of function.
et A = (12, 13, 14, 15, 16, 17) and f : A → Z be a function given by
f(x) = highest prime factor of x.
Find range of f.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
If\[f\left( x \right) = 1 - \frac{1}{x}\] , then write the value of \[f\left( f\left( \frac{1}{x} \right) \right)\]
Let f and g be two functions given by
f = {(2, 4), (5, 6), (8, −1), (10, −3)} and g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, −5)}.
Find the domain of f + g
Which one of the following is not a function?
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right) \text{ and} g\left( x \right) = \frac{3x + x^3}{1 + 3 x^2}\] , then f(g(x)) is equal to
If A = {1, 2, 3} and B = {x, y}, then the number of functions that can be defined from A into B is
If f(x) = cos (log x), then value of \[f\left( x \right) f\left( 4 \right) - \frac{1}{2} \left\{ f\left( \frac{x}{4} \right) + f\left( 4x \right) \right\}\] is
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
Let \[f\left( x \right) = \sqrt{x^2 + 1}\ ] . Then, which of the following is correct?
Check if the following relation is function:
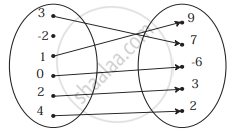
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Check if the following relation is a function.
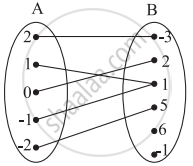
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
Express the following logarithmic equation in exponential form
log2 64 = 6
Express the following logarithmic equation in exponential form
ln e = 1
Write the following expression as sum or difference of logarithm
`log (sqrt(x) root(3)(y))`
Write the following expression as a single logarithm.
ln (x + 2) + ln (x − 2) − 3 ln (x + 5)
Solve for x.
log2 + log(x + 3) – log(3x – 5) = log3
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(0, 0), (1, 1), (1, –1), (4, 2), (4, –2), (9, 3), (9, –3), (16, 4), (16, –4)}
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
Answer the following:
If f(x) = 3x4 – 5x2 + 7 find f(x – 1)
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
Answer the following:
Find the range of the following function.
f(x) = `1/(1 + sqrt(x))`
A function f is defined by f(x) = 2x – 3 find x such that f(x) = f(1 – x)
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
Range of f(x) = `1/(1 - 2 cosx)` is ______.
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
Let f(θ) = sin θ (sin θ + sin 3θ) then ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
