Advertisements
Advertisements
Question
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
Solution
Given:
\[f\left( x \right) = \sqrt{x + 1}\text{ and } g\left( x \right) = \sqrt{9 - x^2}\]
Clearly,
Thus, domain (f) = [1, ∞]
Again,
⇒ \[x \in \left[ - 3, 3 \right]\]
APPEARS IN
RELATED QUESTIONS
If f(x) = x2, find `(f(1.1) - f(1))/((1.1 - 1))`
Define a function as a correspondence between two sets.
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If \[f\left( x \right) = \frac{2x}{1 + x^2}\] , show that f(tan θ) = sin 2θ.
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iv) \[\frac{g}{f}\] Also, find (f + g) (−1), (fg) (0),
Write the domain and range of \[f\left( x \right) = \sqrt{x - \left[ x \right]}\] .
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
If f : Q → Q is defined as f(x) = x2, then f−1 (9) is equal to
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
Let A = {x ∈ R : x ≠ 0, −4 ≤ x ≤ 4} and f : A ∈ R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\] for x ∈ A. Then th (is
If f : R → R be given by for all \[f\left( x \right) = \frac{4^x}{4^x + 2}\] x ∈ R, then
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
Check if the following relation is a function.
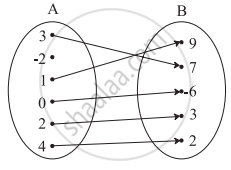
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Show that if f : A → B and g : B → C are one-one, then g ° f is also one-one
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Express the following exponential equation in logarithmic form
`"e"^(1/2)` = 1.6487
Given that log 2 = a and log 3 = b, write `log sqrt(96)` in terms of a and b
If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)2 = 20xy
Select the correct answer from given alternatives.
Find x, if 2log2 x = 4
Answer the following:
A function f : R → R defined by f(x) = `(3x)/5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f–1
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Answer the following:
Show that `7log (15/16) + 6log(8/3) + 5log (2/5) + log(32/25)` = log 3
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
Given the function f: x → x2 – 5x + 6, evaluate f(2)
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
The domain of the function f(x) = `sqrtx` is ______.
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
The range of the function f(x) = `(x^2 - 3x + 2)/(x^3 - 4x^2 + 5x - 2)` is ______
If f(x) = 5x - 3, then f-1(x) is ______
The domain of the real valued function f(x) = `sqrt((x - 2)/(3 - x))` is ______.
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
Range of f(x) = `1/(1 - 2 cosx)` is ______.
Let f(x) and g(x) be two real polynomials of degree 2 and 1 respectively. If f(g(x)) = 8x2 – 2x, and g(f(x)) = 4x2 + 6x + 1, then the value of f(2) + g(2) is ______.
