Advertisements
Advertisements
Question
If f(x) = x2, find `(f(1.1) - f(1))/((1.1 - 1))`
Solution
`f(x)=x^2`
`therefore(f(1.1)-f(1))/(1.1-1)=((1.1)^2-(1)^2)/(1.1-1)=(1.21-1)/0.1=0.21/0.1=2.1`
APPEARS IN
RELATED QUESTIONS
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
Which one of the following is not a function?
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
If \[\left[ x \right]^2 - 5\left[ x \right] + 6 = 0\], where [.] denotes the greatest integer function, then
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Check if the following relation is a function.
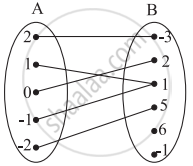
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 3), (4, 1), (2, 2)}
Check if the relation given by the equation represents y as function of x:
3x − 6 = 21
If f(m) = m2 − 3m + 1, find f(− x)
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Find the domain and range of the following function.
f(x) = `sqrt((x - 2)(5 - x)`
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Express the following exponential equation in logarithmic form
54° = 1
Express the following logarithmic equation in exponential form
ln 1 = 0
Write the following expression as a single logarithm.
`1/3 log (x - 1) + 1/2 log (x)`
Given that log 2 = a and log 3 = b, write `log sqrt(96)` in terms of a and b
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
If f(x) = 3x + 5, g(x) = 6x − 1, then find (fg) (3)
The equation logx2 16 + log2x 64 = 3 has,
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
Answer the following:
A function f is defined as f(x) = 4x + 5, for – 4 ≤ x < 0. Find the values of f(–1), f(–2), f(0), if they exist
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
Solve : `sqrt(log_2 x^4) + 4log_4 sqrt(2/x)` = 2
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Answer the following:
Find the domain of the following function.
f(x) = x!
If the domain of function f(a) = a2 - 4a + 8 is (-∞, ∞), then the range of function is ______
If f(x) = 5x - 3, then f-1(x) is ______
Let A and B be any two sets such that n(B) = p, n(A) = q then the total number of functions f : A → B is equal to ______.
Find the domain of the following function given by:
f(x) = `(3x)/(2x - 8)`
Find the range of the following functions given by f(x) = 1 – |x – 2|
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
The range of the function y = `1/(2 - sin3x)` is ______.
