Advertisements
Advertisements
प्रश्न
The domain of definition of the function f(x) = log |x| is
विकल्प
(a) R
(b) (−∞, 0)
(c) (0, ∞)
(d) R − {0}
उत्तर
(d) R − {0}
f(x) = log |x|
\[\text{ For f(x) to be defined,} \]
\[\left| x \right| > 0, \text{ which is always true . } \]
\[\text{ But } \left| x \right| \neq 0\]
\[ \Rightarrow x \neq 0\]
\[\text{ Thus, dom }(f) = R - {0} . \]
APPEARS IN
संबंधित प्रश्न
If f(x) = x2, find \[\frac{f\left( 1 . 1 \right) - f\left( 1 \right)}{\left( 1 . 1 \right) - 1}\]
If f(x) = x2 − 3x + 4, then find the values of x satisfying the equation f(x) = f(2x + 1).
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If f, g and h are real functions defined by
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
If f : Q → Q is defined as f(x) = x2, then f−1 (9) is equal to
If x ≠ 1 and \[f\left( x \right) = \frac{x + 1}{x - 1}\] is a real function, then f(f(f(2))) is
If \[f\left( x \right) = \frac{\sin^4 x + \cos^2 x}{\sin^2 x + \cos^4 x}\] for x ∈ R, then f (2002) =
If f : R → R be given by for all \[f\left( x \right) = \frac{4^x}{4^x + 2}\] x ∈ R, then
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
Which of the following relations are functions? If it is a function determine its domain and range:
{(0, 0), (1, 1), (1, −1), (4, 2), (4, −2), (9, 3), (9, −3), (16, 4), (16, −4)}
Find x, if g(x) = 0 where g(x) = x3 − 2x2 − 5x + 6
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
Find the domain and range of the following function.
g(x) = `(x + 4)/(x - 2)`
Express the following exponential equation in logarithmic form
25 = 32
Express the following exponential equation in logarithmic form
e2 = 7.3890
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Prove that `"b"^(log_"b""a"` = a
Solve for x.
log2 + log(x + 3) – log(3x – 5) = log3
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Answer the following:
A function f : R → R defined by f(x) = `(3x)/5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f–1
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
Answer the following:
Find the range of the following function.
f(x) = [x] – x
A graph representing the function f(x) is given in it is clear that f(9) = 2
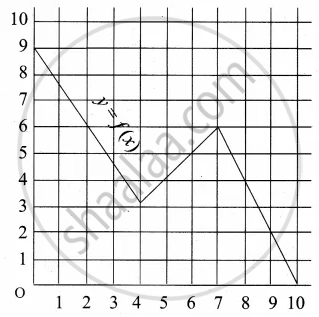
For what value of x is f(x) = 1?
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
A function f is defined by f(x) = 2x – 3 find x such that f(x) = f(1 – x)
If f(x) = 5x - 3, then f-1(x) is ______
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
Let f(θ) = sin θ (sin θ + sin 3θ) then ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
