Advertisements
Advertisements
प्रश्न
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
विकल्प
(a) (−∞, −2] ∪ [2, ∞)
(b) [−1, 1]
(c) ϕ
(d) None of these
उत्तर
(c) ϕ
\[\text{ For f(x) to be defined,} \]
\[x + 2 \neq 0\]
\[ \Rightarrow x \neq - 2 . . . (1)\]
\[\text{ And } 1 + x \neq 0\]
\[ \Rightarrow x \neq - 1 . . . . (2)\]
\[\text{ Also } , \frac{x - 2}{x + 2} \geq 0\]
\[ \Rightarrow \frac{(x - 2)(x + 2)}{(x + 2 )^2} \geq 0\]
\[ \Rightarrow (x - 2)(x + 2) \geq 0\]
\[ \Rightarrow x \in ( - \infty , - 2) \cup [2, \infty ) . . . (3)\]
\[\text{ And } \frac{1 - x}{1 + x} \geq 0\]
\[ \Rightarrow \frac{(1 - x)(1 + x)}{(1 + x )^2} \geq 0\]
\[ \Rightarrow (1 - x)(1 + x) \geq 0\]
\[ \Rightarrow x \in ( - \infty , - 1) \cup [1, \infty ) . . . (4)\]
\[\text{ From (1), (2), (3) and (4), we get,} \]
\[x \in \phi . \]
\[\text{ Thus, dom } (f(x)) = \phi . \]
APPEARS IN
संबंधित प्रश्न
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
- {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
- {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
- {(1, 3), (1, 5), (2, 5)}
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
Let f : R → R and g : C → C be two functions defined as f(x) = x2 and g(x) = x2. Are they equal functions?
f, g, h are three function defined from R to R as follow:
(iii) h(x) = x2 + 1
Find the range of function.
Write the range of the real function f(x) = |x|.
Write the domain and range of \[f\left( x \right) = \sqrt{x - \left[ x \right]}\] .
If 2f (x) − \[3f\left( \frac{1}{x} \right) = x^2\] (x ≠ 0), then f(2) is equal to
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
If f : R → R be given by for all \[f\left( x \right) = \frac{4^x}{4^x + 2}\] x ∈ R, then
The domain of definition of the function \[f\left( x \right) = \sqrt{x - 1} + \sqrt{3 - x}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
Check if the relation given by the equation represents y as function of x:
3x − 6 = 21
If f(m) = m2 − 3m + 1, find `f(1/2)`
If f(m) = m2 − 3m + 1, find f(− x)
Find the domain and range of the following function.
f(x) = `sqrt((x - 2)(5 - x)`
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following exponential equation in logarithmic form
`"e"^(1/2)` = 1.6487
Express the following logarithmic equation in exponential form
`log_(1/2) (8)` = – 3
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f + g) (x)
Select the correct answer from given alternatives.
If log10(log10(log10x)) = 0 then x =
Answer the following:
Show that, `log ("a"^2/"bc") + log ("b"^2/"ca") + log ("c"^2/"ab")` = 0
Answer the following:
Simplify, log (log x4) – log (log x)
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the domain of the following function.
f(x) = 5–xPx–1
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
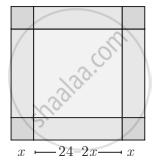
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
The domain of the function f(x) = `sqrtx` is ______.
If the domain of function f(a) = a2 - 4a + 8 is (-∞, ∞), then the range of function is ______
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Find the range of the following functions given by f(x) = 1 – |x – 2|
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
Range of f(x) = `1/(1 - 2 cosx)` is ______.
The domain of the function f defined by f(x) = `sqrt(4 - x) + 1/sqrt(x^2 - 1)` is equal to ______.
Let f(x) and g(x) be two real polynomials of degree 2 and 1 respectively. If f(g(x)) = 8x2 – 2x, and g(f(x)) = 4x2 + 6x + 1, then the value of f(2) + g(2) is ______.
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
The period of the function
f(x) = `(sin 8x cos x - sin 6x cos 3x)/(cos 2x cos x - sin 3x sin 4x)` is ______.
