Advertisements
Advertisements
प्रश्न
Find the range of the following functions given by f(x) = 1 – |x – 2|
उत्तर
For real value of f
|x – 2| ≥ 0
Adding negative sign, we get
Or –|x – 2| ≤ 0
Adding 1 we get
⇒ 1 – |x – 2| ≤ 1
Or f(x) ≤ 1
⇒ f(x) ∈ `(–oo, 1]`
Therefore, the range of f = `(–oo, 1]`
APPEARS IN
संबंधित प्रश्न
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
If for non-zero x, af(x) + bf \[\left( \frac{1}{x} \right) = \frac{1}{x} - 5\] , where a ≠ b, then find f(x).
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] . Then write the value of α satisfying f(f(x)) = x for all x ≠ −1.
Let f : R → R be defined by f(x) = 2x + |x|. Then f(2x) + f(−x) − f(x) =
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
Let \[f\left( x \right) = \sqrt{x^2 + 1}\ ] . Then, which of the following is correct?
If f(x) = 3x + a and f(1) = 7 find a and f(4).
Check if the following relation is a function.
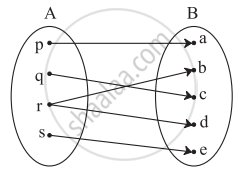
Check if the relation given by the equation represents y as function of x:
2y + 10 = 0
Find x, if g(x) = 0 where g(x) = x3 − 2x2 − 5x + 6
Express the following exponential equation in logarithmic form
e2 = 7.3890
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Answer the following:
Find the domain of the following function.
f(x) = 5–xPx–1
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
Answer the following:
Find the range of the following function.
f(x) = [x] – x
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
Given the function f: x → x2 – 5x + 6, evaluate f(2)
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Find the range of the following functions given by `sqrt(16 - x^2)`
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f – g)(x)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
The value of the function f(x) = `(x^2 - 3x + 2)/(x^2 + x - 6)` lies in the interval
