Advertisements
Advertisements
प्रश्न
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
उत्तर
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
(f ° g) (x) = f(g(x)) = `"f"(x/(1 - x))`
= `(x/(1 - x))/(x/(1 - x) + 1)`
= `x/(x + 1 - x)`
= x
(g ° f) (x) = g(f(x))
= `"g"(x/(x + 1))`
= `(x/(x + 1))/(1 - x/(x + 1))`
= `x/(x + 1 - x)`
= x
APPEARS IN
संबंधित प्रश्न
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
If f(x) = (x − a)2 (x − b)2, find f(a + b).
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
If f, g and h are real functions defined by
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, −4), (4, 2), (5, 1)} and g = {(1, 0), (2, 2), (3, −1), (4, 4), (5, 3)}
Find the domain of fg.
Let A = {1, 2, 3} and B = {2, 3, 4}. Then which of the following is a function from A to B?
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
If x ≠ 1 and \[f\left( x \right) = \frac{x + 1}{x - 1}\] is a real function, then f(f(f(2))) is
f is a real valued function given by \[f\left( x \right) = 27 x^3 + \frac{1}{x^3}\] and α, β are roots of \[3x + \frac{1}{x} = 12\] . Then,
If \[f\left( x \right) = 64 x^3 + \frac{1}{x^3}\] and α, β are the roots of \[4x + \frac{1}{x} = 3\] . Then,
The domain of the function
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
Let \[f\left( x \right) = \sqrt{x^2 + 1}\ ] . Then, which of the following is correct?
Check if the following relation is function:
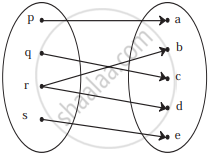
Check if the following relation is function:
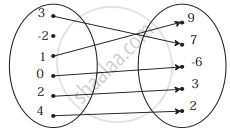
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
If f(m) = m2 − 3m + 1, find f(x + 1)
If f(m) = m2 − 3m + 1, find f(− x)
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Find x, if g(x) = 0 where g(x) = x3 − 2x2 − 5x + 6
Find x, if f(x) = g(x) where f(x) = x4 + 2x2, g(x) = 11x2
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Express the area A of circle as a function of its diameter d
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Write the following expression as sum or difference of logarithm
`log (sqrt(x) root(3)(y))`
Prove that `"b"^(log_"b""a"` = a
If `log((x + y)/3) = 1/2 log x + 1/2 logy`, show that `x/y + y/x` = 7
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
The domain of the function f(x) = `sqrtx` is ______.
Domain of function f(x) = cos–1 6x is ______.
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
The domain of the function f given by f(x) = `(x^2 + 2x + 1)/(x^2 - x - 6)` is ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
