Advertisements
Advertisements
प्रश्न
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
उत्तर
Given that,
`f(x) = sin|x|`
where `(-pi)/4 le x le pi/4`
we divide the range into two parts,
(a) `(-pi/4)< x < 0`
`⇒ |x| = -1`
Then `f(x) = sin(-1) = - sin 1`
(b) `0 < x < (pi/4)`
`⇒ |x| = 0`
Then, `f(x) = sin0 = 0`
Thus, the range of f(x) becomes {0, −sin1}
APPEARS IN
संबंधित प्रश्न
If for non-zero x, af(x) + bf \[\left( \frac{1}{x} \right) = \frac{1}{x} - 5\] , where a ≠ b, then find f(x).
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
If f(x) = cos [π2]x + cos [−π2] x, where [x] denotes the greatest integer less than or equal to x, then write the value of f(π).
Let f and g be two functions given by
f = {(2, 4), (5, 6), (8, −1), (10, −3)} and g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, −5)}.
Find the domain of f + g
If f(x) = cos (log x), then the value of f(x2) f(y2) −
The range of f(x) = cos [x], for π/2 < x < π/2 is
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
Let A = {x ∈ R : x ≠ 0, −4 ≤ x ≤ 4} and f : A ∈ R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\] for x ∈ A. Then th (is
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
The range of the function f(x) = |x − 1| is
If \[\left[ x \right]^2 - 5\left[ x \right] + 6 = 0\], where [.] denotes the greatest integer function, then
Check if the following relation is function:
If f(m) = m2 − 3m + 1, find f(−3)
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(2)
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 1), (2, 1), (3, 1), (4, 1)}
If f(m) = m2 − 3m + 1, find f(−3)
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Find x, if g(x) = 0 where g(x) = x3 − 2x2 − 5x + 6
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Express the following exponential equation in logarithmic form
25 = 32
Express the following exponential equation in logarithmic form
10−2 = 0.01
Solve for x.
log2 + log(x + 3) – log(3x – 5) = log3
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
Select the correct answer from given alternatives
The domain of `1/([x] - x)` where [x] is greatest integer function is
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Answer the following:
If f(x) = log(1 – x), 0 ≤ x < 1 show that `"f"(1/(1 + x))` = f(1 – x) – f(– x)
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
A graph representing the function f(x) is given in it is clear that f(9) = 2
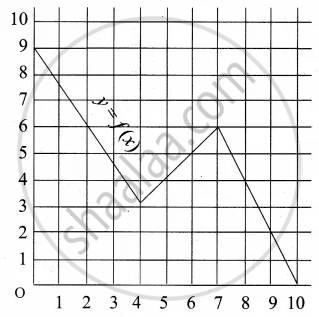
Describe the following Domain
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
A function f is defined by f(x) = 2x – 3 find `("f"(0) + "f"(1))/2`
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
Find the range of the following functions given by f(x) = 1 – |x – 2|
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
