Advertisements
Advertisements
प्रश्न
Check if the following relation is function:
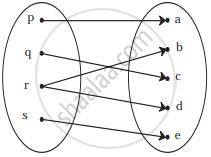
उत्तर
No.
Reason:
An element of set A has been assigned more than one element from set B.
APPEARS IN
संबंधित प्रश्न
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iv) \[\frac{g}{f}\] Also, find (f + g) (−1), (fg) (0),
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
If ƒ(m) = m2 − 3m + 1, find f(x + 1)
Check if the following relation is a function.
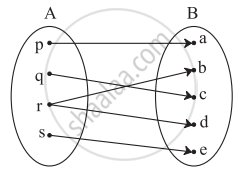
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also find its domain
Express the following exponential equation in logarithmic form
10−2 = 0.01
If f(x) = 3x + 5, g(x) = 6x − 1, then find (fg) (3)
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Answer the following:
A function f : R → R defined by f(x) = `(3x)/5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f–1
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
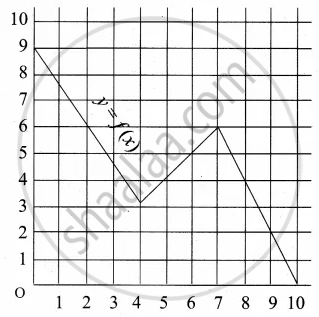
What is the image of 6 under f?
Find the range of the following functions given by f(x) = `3/(2 - x^2)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
