Advertisements
Advertisements
प्रश्न
Check if the following relation is a function.
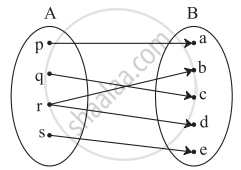
उत्तर
No
Reason:
An element of set A has been assigned more than one element from set B.
APPEARS IN
संबंधित प्रश्न
Define a function as a correspondence between two sets.
Let A = [p, q, r, s] and B = [1, 2, 3]. Which of the following relations from A to B is not a function?
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
Write the range of the function f(x) = ex−[x], x ∈ R.
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, −4), (4, 2), (5, 1)} and g = {(1, 0), (2, 2), (3, −1), (4, 4), (5, 3)}
Find the domain of fg.
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
If 2f (x) − \[3f\left( \frac{1}{x} \right) = x^2\] (x ≠ 0), then f(2) is equal to
Check if the following relation is function:

Which of the following relations are functions? If it is a function determine its domain and range:
{(1, 1), (3, 1), (5, 2)}
A function f is defined as follows: f(x) = 4x + 5, for −4 ≤ x < 0. Find the values of f(−1), f(−2), f(0), if they exist.
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 1), (2, 1), (3, 1), (4, 1)}
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Express the area A of circle as a function of its radius r
Express the area A of circle as a function of its circumference C.
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Answer the following:
A function f is defined as f(x) = 4x + 5, for – 4 ≤ x < 0. Find the values of f(–1), f(–2), f(0), if they exist
Answer the following:
If f(x) = 3x4 – 5x2 + 7 find f(x – 1)
Answer the following:
Find x, if x = 33log32
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
If f(x) = log(1 – x), 0 ≤ x < 1 show that `"f"(1/(1 + x))` = f(1 – x) – f(– x)
Answer the following:
Find the domain of the following function.
f(x) = x!
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
Let f = {(x, y) | x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?
Given the function f: x → x2 – 5x + 6, evaluate f(2)
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
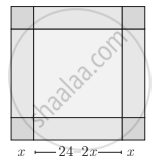
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find the height of a person whose forehand length is 40 cm
Let A = {1, 2, 3, 4} and B = N. Let f : A → B be defined by f(x) = x3 then, find the range of f
Find the range of the following functions given by `|x - 4|/(x - 4)`
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Find the range of the following functions given by f(x) = `3/(2 - x^2)`
Let f(x) = `sqrt(1 + x^2)`, then ______.
Let f(θ) = sin θ (sin θ + sin 3θ) then ______.
The range of the function f(x) = `""^(7 - x)P_(x - 3)` is ______.
