Advertisements
Advertisements
प्रश्न
Write the range of the function f(x) = ex−[x], x ∈ R.
उत्तर
f(x) = ex−[x], x ∈ R
\[\text { We know that x - [x] = {x}, which is the fractional part of any number x .} \]
\[\text{ Thus} , f(x) = e^{{x}} \]
\[\text{ Also} , 0 \leq {x} < 1\]
\[ \Rightarrow e^0 \leq e^{{x}} < e^1 \]
\[ \Rightarrow 1 \leq f(x) < e\]
\[\text{ Thus range of f(x) is } [1, e) . \]
APPEARS IN
संबंधित प्रश्न
find: f(1), f(−1), f(0) and f(2).
Let f : R → R and g : C → C be two functions defined as f(x) = x2 and g(x) = x2. Are they equal functions?
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(v) \[\frac{g}{f}\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
The range of the function \[f\left( x \right) = \frac{x^2 - x}{x^2 + 2x}\] is
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
Let A = {x ∈ R : x ≠ 0, −4 ≤ x ≤ 4} and f : A ∈ R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\] for x ∈ A. Then th (is
If f(m) = m2 − 3m + 1, find f(0)
Which of the following relations are functions? If it is a function determine its domain and range:
{(0, 0), (1, 1), (1, −1), (4, 2), (4, −2), (9, 3), (9, −3), (16, 4), (16, −4)}
Which of the following relations are functions? If it is a function determine its domain and range:
{(1, 1), (3, 1), (5, 2)}
A function f is defined as follows: f(x) = 4x + 5, for −4 ≤ x < 0. Find the values of f(−1), f(−2), f(0), if they exist.
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Check if the relation given by the equation represents y as function of x:
2y + 10 = 0
Check if the relation given by the equation represents y as function of x:
3x − 6 = 21
Find x, if g(x) = 0 where g(x) = `(18 -2x^2)/7`
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Find the domain and range of the following function.
f(x) = `sqrt(16 - x^2)`
Express the following exponential equation in logarithmic form
54° = 1
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
Write the following expression as sum or difference of logarithm
In `(("a"^3 ("a" - 2)^2)/sqrt("b"^2 + 5))`
If f(x) = 3x + 5, g(x) = 6x − 1, then find `("f"/"g") (x)` and its domain
Select the correct answer from given alternative.
The domain and range of f(x) = 2 − |x − 5| is
Answer the following:
Find value of `(3 + log_10 343)/(2 + 1/2 log_10 (49/4) + 1/2 log_10 (1/25)`
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
Answer the following:
Find the range of the following function.
f(x) = 1 + 2x + 4x
Given the function f: x → x2 – 5x + 6, evaluate f(2a)
A graph representing the function f(x) is given in it is clear that f(9) = 2
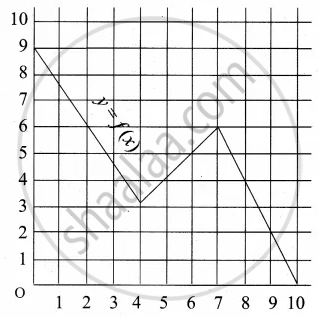
What is the image of 6 under f?
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
Find the range of the following functions given by `|x - 4|/(x - 4)`
If f(x) = `x^3 - 1/x^3`, then `f(x) + f(1/x)` is equal to ______.
Find the domain of the following functions given by f(x) = `1/sqrt(x + |x|)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
If f(x) = y = `(ax - b)/(cx - a)`, then prove that f(y) = x.
The value of the function f(x) = `(x^2 - 3x + 2)/(x^2 + x - 6)` lies in the interval
If f(x) = x3 – 1 and domain of f = {0, 1, 2, 3}, then domain of f–1 is ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
