Advertisements
Advertisements
प्रश्न
Express the following exponential equation in logarithmic form
54° = 1
उत्तर
| Exponential form | Logarithmic form |
| 54° = 1 | 0 = log54 1 |
APPEARS IN
संबंधित प्रश्न
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
- {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
- {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
- {(1, 3), (1, 5), (2, 5)}
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
What is the fundamental difference between a relation and a function? Is every relation a function?
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(ii) g − f
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
Let A = {1, 2, 3} and B = {2, 3, 4}. Then which of the following is a function from A to B?
The range of f(x) = cos [x], for π/2 < x < π/2 is
The range of the function f(x) = |x − 1| is
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
Check if the following relation is function:
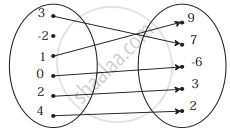
If f(m) = m2 − 3m + 1, find f(−3)
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 3), (4, 1), (2, 2)}
If f(m) = m2 − 3m + 1, find f(−3)
Find the domain and range of the following function.
f(x) = `sqrt((x - 2)(5 - x)`
Express the area A of a square as a function of its perimeter P
Let f be a subset of Z × Z defined by f = {(ab, a + b) : a, b ∈ Z}. Is f a function from Z to Z? Justify?
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Find the domain of f(x) = log10 (x2 − 5x + 6)
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
Select the correct answer from given alternatives.
If f : R → R is defined by f(x) = x3 then f–1 (8) is equal to :
Select the correct answer from given alternative.
The domain and range of f(x) = 2 − |x − 5| is
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(0, 0), (1, 1), (1, –1), (4, 2), (4, –2), (9, 3), (9, –3), (16, 4), (16, –4)}
Answer the following:
If f(x) = 3x + a and f(1) = 7 find a and f(4)
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
A graph representing the function f(x) is given in it is clear that f(9) = 2
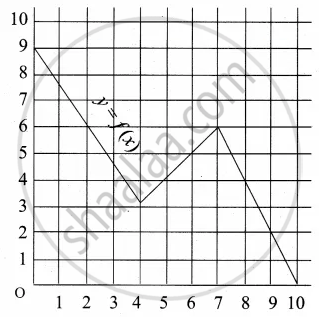
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
A function f is defined by f(x) = 2x – 3 find `("f"(0) + "f"(1))/2`
A function f is defined by f(x) = 2x – 3 find x such that f(x) = 0
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
If the domain of function f(a) = a2 - 4a + 8 is (-∞, ∞), then the range of function is ______
The range of the function f(x) = `(x^2 - 3x + 2)/(x^3 - 4x^2 + 5x - 2)` is ______
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Find the domain of the following function given by:
f(x) = `(3x)/(2x - 8)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
The range of the function f(x) = `""^(7 - x)P_(x - 3)` is ______.
