Advertisements
Advertisements
प्रश्न
Express the following exponential equation in logarithmic form
25 = 32
उत्तर
25 = 32
∴ 5 = log2 32 …[By definition of logarithm]
i.e. log2 32 = 5
APPEARS IN
संबंधित प्रश्न
f, g, h are three function defined from R to R as follow:
(i) f(x) = x2
Find the range of function.
If \[f\left( x \right) = \frac{x - 1}{x + 1}\] , then show that
(i) \[f\left( \frac{1}{x} \right) = - f\left( x \right)\]
(ii) \[f\left( - \frac{1}{x} \right) = - \frac{1}{f\left( x \right)}\]
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] . Then write the value of α satisfying f(f(x)) = x for all x ≠ −1.
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right) \text{ and} g\left( x \right) = \frac{3x + x^3}{1 + 3 x^2}\] , then f(g(x)) is equal to
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right)\] , then \[f\left( \frac{2x}{1 + x^2} \right)\] is equal to
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
The domain of the function
The domain of definition of the function f(x) = log |x| is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
Check if the following relation is function:

Which of the following relations are functions? If it is a function determine its domain and range:
{(1, 1), (3, 1), (5, 2)}
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
If f(m) = m2 − 3m + 1, find f(−3)
Find x, if g(x) = 0 where g(x) = `(18 -2x^2)/7`
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Express the area A of circle as a function of its circumference C.
lf f(x) = 3(4x+1), find f(– 3)
Express the following exponential equation in logarithmic form
10−2 = 0.01
Express the following logarithmic equation in exponential form
log10 (0.001) = −3
Find the domain of f(x) = ln (x − 5)
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Answer the following:
A function f is defined as f(x) = 4x + 5, for – 4 ≤ x < 0. Find the values of f(–1), f(–2), f(0), if they exist
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Find the domain of the following function.
f(x) = 5–xPx–1
A graph representing the function f(x) is given in it is clear that f(9) = 2
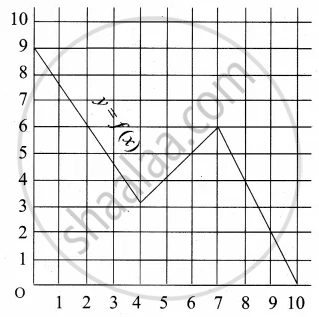
Describe the following Range
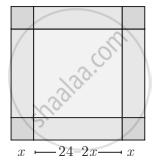
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Write an expression for gf(x) in its simplest form
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
Let f and g be two functions given by f = {(2, 4), (5, 6), (8, – 1), (10, – 3)} g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, – 5)} then. Domain of f + g is ______.
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
The domain of the function f defined by f(x) = `sqrt(4 - x) + 1/sqrt(x^2 - 1)` is equal to ______.
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
