Advertisements
Advertisements
प्रश्न
Find the domain of f(x) = ln (x − 5)
उत्तर
f(x) = ln (x − 5)
f is defined, when x – 5 > 0
∴ x > 5
Domain of f = `(5, ∞)`
APPEARS IN
संबंधित प्रश्न
If f(x) = x2, find `(f(1.1) - f(1))/((1.1 - 1))`
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(c) f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iv) \[\frac{g}{f}\] Also, find (f + g) (−1), (fg) (0),
If f : Q → Q is defined as f(x) = x2, then f−1 (9) is equal to
Which of the following are functions?
If f(x) = cos (log x), then value of \[f\left( x \right) f\left( 4 \right) - \frac{1}{2} \left\{ f\left( \frac{x}{4} \right) + f\left( 4x \right) \right\}\] is
If 2f (x) − \[3f\left( \frac{1}{x} \right) = x^2\] (x ≠ 0), then f(2) is equal to
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
The domain of the function
Check if the following relation is function:

Check if the following relation is function:
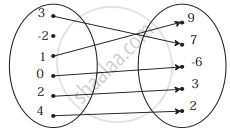
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
If f(m) = m2 − 3m + 1, find f(−3)
If f(m) = m2 − 3m + 1, find f(− x)
Find the domain and range of the following function.
g(x) = `(x + 4)/(x - 2)`
Check the injectivity and surjectivity of the following function.
f : R → R given by f(x) = x3
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Express the following exponential equation in logarithmic form
10−2 = 0.01
Express the following exponential equation in logarithmic form
e–x = 6
Write the following expression as sum or difference of logarithm
`log (sqrt(x) root(3)(y))`
Write the following expression as a single logarithm.
`1/3 log (x - 1) + 1/2 log (x)`
Prove that alogcb = blogca
Select the correct answer from given alternatives.
Find x, if 2log2 x = 4
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Answer the following:
Find the range of the following function.
f(x) = `1/(1 + sqrt(x))`
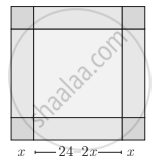
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
Let f : R → R be defined by
f(x) = `{(3x; x > 2),(2x^2; 1 ≤ x ≤ 2), (4x; x < 1):}`
Then f(-2) + f(1) + f(3) is ______
Redefine the function which is given by f(x) = `|x - 1| + |1 + x|, -2 ≤ x ≤ 2`
If f(x) = `x^3 - 1/x^3`, then `f(x) + f(1/x)` is equal to ______.
Let A and B be any two sets such that n(B) = p, n(A) = q then the total number of functions f : A → B is equal to ______.
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
