Advertisements
Advertisements
प्रश्न
The domain of the function
विकल्प
(a) \[\left[ - \sqrt{3}, \sqrt{3} \right]\]
(b) \[\left[ - 1 - \sqrt{3}, - 1 + \sqrt{3} \right]\]
(c) [−2, 2]
(d) \[\left[ - 2 - \sqrt{3}, - 2 + \sqrt{3} \right]\]
उत्तर
(b) \[\left[ - 1 - \sqrt{3}, - 1 + \sqrt{3} \right]\]
\[ x^2 + 2x - 2 \leq 0\]
\[ \Rightarrow x^2 - 2x - 2 + 1 - 1 \leq 0\]
\[ \Rightarrow \left( x - 1 \right)^2 - \left( \sqrt{3} \right)^2 \leq 0\]
\[ \Rightarrow \left[ x - \left( - 1 - \sqrt{3} \right) \right]\left[ x - \left( - 1 + \sqrt{3} \right) \right] \leq 0\]
\[ \Rightarrow \left( - 1 - \sqrt{3} \right) \leq x \leq \left( - 1 + \sqrt{3} \right)\]
\[\text{ Thus, dom} (f) = \left[ - 1 - \sqrt{3}, - 1 + \sqrt{3} \right] . \]
APPEARS IN
संबंधित प्रश्न
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(a) the image set of the domain of f
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vii) f2 + 7f
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iv) \[\frac{g}{f}\] Also, find (f + g) (−1), (fg) (0),
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
If f(x) = sin [π2] x + sin [−π]2 x, where [x] denotes the greatest integer less than or equal to x, then
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
Check if the relation given by the equation represents y as function of x:
x + y2 = 9
Find x, if g(x) = 0 where g(x) = `(18 -2x^2)/7`
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Express the area A of a square as a function of its perimeter P
Express the following exponential equation in logarithmic form
`9^(3/2)` = 27
Express the following logarithmic equation in exponential form
`log_5 1/25` = – 2
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
Write the following expression as a single logarithm.
`1/3 log (x - 1) + 1/2 log (x)`
Prove that `"b"^(log_"b""a"` = a
If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)2 = 20xy
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
Given the function f: x → x2 – 5x + 6, evaluate f(2)
A graph representing the function f(x) is given in it is clear that f(9) = 2
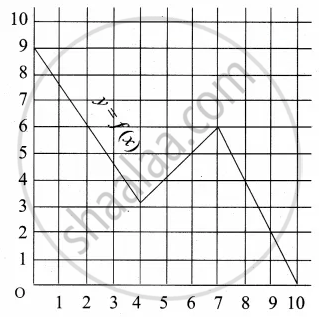
Describe the following Domain
A graph representing the function f(x) is given in it is clear that f(9) = 2
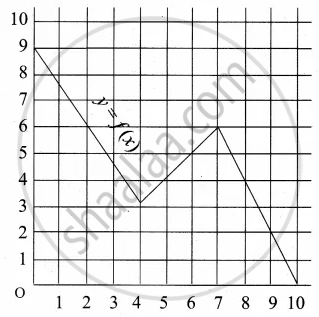
What is the image of 6 under f?
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
If the domain of function f(a) = a2 - 4a + 8 is (-∞, ∞), then the range of function is ______
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Find the range of the following functions given by f(x) = `3/(2 - x^2)`
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
The period of the function
f(x) = `(sin 8x cos x - sin 6x cos 3x)/(cos 2x cos x - sin 3x sin 4x)` is ______.
