Advertisements
Advertisements
प्रश्न
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
उत्तर
L.H.S. = logy (x3) logz (y4) logx (z5)
= (3 logy x) (4 logz y) (5 logx z)
= `60 ((logx)/(logy)) ((logy)/(logz)) ((logz)/(logx))`
= 60
= R.H.S.
APPEARS IN
संबंधित प्रश्न
If \[f\left( x \right) = x^3 - \frac{1}{x^3}\] , show that
If \[f\left( x \right) = \frac{x - 1}{x + 1}\] , then show that
(i) \[f\left( \frac{1}{x} \right) = - f\left( x \right)\]
(ii) \[f\left( - \frac{1}{x} \right) = - \frac{1}{f\left( x \right)}\]
Write the range of the real function f(x) = |x|.
If\[f\left( x \right) = 1 - \frac{1}{x}\] , then write the value of \[f\left( f\left( \frac{1}{x} \right) \right)\]
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
The range of f(x) = cos [x], for π/2 < x < π/2 is
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
Let A = {x ∈ R : x ≠ 0, −4 ≤ x ≤ 4} and f : A ∈ R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\] for x ∈ A. Then th (is
If f(x) = sin [π2] x + sin [−π]2 x, where [x] denotes the greatest integer less than or equal to x, then
If f(m) = m2 − 3m + 1, find f(0)
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 3), (4, 1), (2, 2)}
Check if the relation given by the equation represents y as function of x:
x + y2 = 9
If f(m) = m2 − 3m + 1, find f(− x)
Find the domain and range of the following function.
g(x) = `(x + 4)/(x - 2)`
Find the domain and range of the following function.
f(x) = `root(3)(x + 1)`
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Find the domain of f(x) = ln (x − 5)
Write the following expression as a single logarithm.
5 log x + 7 log y − log z
If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)2 = 20xy
If f(x) = 3x + 5, g(x) = 6x − 1, then find (fg) (3)
Answer the following:
Find whether the following function is one-one
f : R − {3} → R defined by f(x) = `(5x + 7)/(x - 3)` for x ∈ R − {3}
Answer the following:
A function f : R → R defined by f(x) = `(3x)/5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f–1
Answer the following:
Find value of `(3 + log_10 343)/(2 + 1/2 log_10 (49/4) + 1/2 log_10 (1/25)`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Let f = {(x, y) | x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?
A graph representing the function f(x) is given in it is clear that f(9) = 2
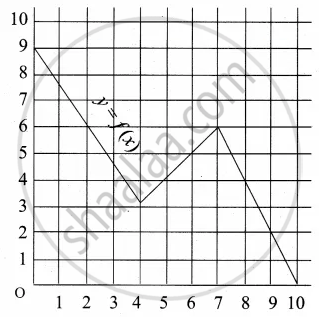
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
A graph representing the function f(x) is given in it is clear that f(9) = 2
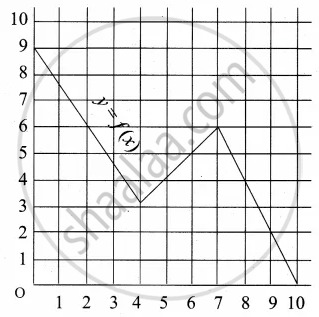
For what value of x is f(x) = 1?
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
The domain of the function f(x) = log3+x (x2 - 1) is ______.
Find the domain of the following functions given by f(x) = `1/sqrt(x + |x|)`
Find the range of the following functions given by f(x) = 1 – |x – 2|
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
If f(x) = `(x - 1)/(x + 1)`, then show that `f(- 1/x) = (-1)/(f(x))`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
If f(x) = x3 – 1 and domain of f = {0, 1, 2, 3}, then domain of f–1 is ______.
