Advertisements
Advertisements
प्रश्न
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
उत्तर
It is given that A and B are two sets such that n(A) = p and n(B) = q.
Now, any element of set A, say ai (1 ≤ i ≤ p), is related with an element of set B in q ways. Similarly, other elements of set A are related with an element of set B in q ways.
Thus, every element of set A is related with every element of set B in q ways.
∴ Total number of functions from A to B = q × q × q × ... × q (p times) = qp
APPEARS IN
संबंधित प्रश्न
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
- {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
- {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
- {(1, 3), (1, 5), (2, 5)}
If \[f\left( x \right) = \frac{x - 1}{x + 1}\] , then show that
(i) \[f\left( \frac{1}{x} \right) = - f\left( x \right)\]
(ii) \[f\left( - \frac{1}{x} \right) = - \frac{1}{f\left( x \right)}\]
Write the domain and range of function f(x) given by
The range of f(x) = cos [x], for π/2 < x < π/2 is
If A = {1, 2, 3} and B = {x, y}, then the number of functions that can be defined from A into B is
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
Check if the following relation is function:
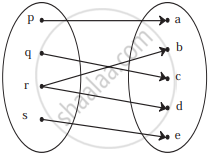
Which of the following relations are functions? If it is a function determine its domain and range:
{(0, 0), (1, 1), (1, −1), (4, 2), (4, −2), (9, 3), (9, −3), (16, 4), (16, −4)}
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Check if the following relation is a function.
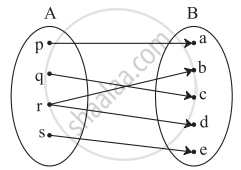
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
Check if the relation given by the equation represents y as function of x:
3x − 6 = 21
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also find its domain
Express the following exponential equation in logarithmic form
`"e"^(1/2)` = 1.6487
Write the following expression as a single logarithm.
5 log x + 7 log y − log z
Solve for x.
log2 x + log4 x + log16 x = `21/4`
Select the correct answer from given alternatives.
If f : R → R is defined by f(x) = x3 then f–1 (8) is equal to :
Select the correct answer from given alternatives
The domain of `1/([x] - x)` where [x] is greatest integer function is
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Answer the following:
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 5
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If f(x) = log(1 – x), 0 ≤ x < 1 show that `"f"(1/(1 + x))` = f(1 – x) – f(– x)
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
Answer the following:
Find the range of the following function.
f(x) = [x] – x
A function f is defined by f(x) = 2x – 3 find x such that f(x) = f(1 – x)
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
Let A and B be any two sets such that n(B) = p, n(A) = q then the total number of functions f : A → B is equal to ______.
Find the domain of the following functions given by f(x) = `1/sqrt(1 - cos x)`
Redefine the function f(x) = x − 2 + 2 + x , – 3 ≤ x ≤ 3
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
The domain of the function f given by f(x) = `(x^2 + 2x + 1)/(x^2 - x - 6)` is ______.
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
