Advertisements
Advertisements
Question
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
Solution
L.H.S. = logy (x3) logz (y4) logx (z5)
= (3 logy x) (4 logz y) (5 logx z)
= `60 ((logx)/(logy)) ((logy)/(logz)) ((logz)/(logx))`
= 60
= R.H.S.
APPEARS IN
RELATED QUESTIONS
Let f : R → R and g : C → C be two functions defined as f(x) = x2 and g(x) = x2. Are they equal functions?
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(ii) g − f
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(v) \[\frac{g}{f}\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iii) \[\frac{f}{g}\]
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
If \[f\left( x \right) = \frac{\sin^4 x + \cos^2 x}{\sin^2 x + \cos^4 x}\] for x ∈ R, then f (2002) =
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
Check if the following relation is function:
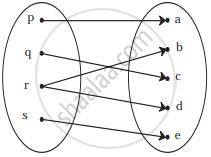
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(0)
If f(m) = m2 − 3m + 1, find f(0)
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also find its domain
Express the following exponential equation in logarithmic form
54° = 1
Express the following logarithmic equation in exponential form
`log_(1/2) (8)` = – 3
Find the domain of f(x) = log10 (x2 − 5x + 6)
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
Solve for x.
2 log10 x = `1 + log_10 (x + 11/10)`
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
Answer the following:
A function f : R → R defined by f(x) = `(3x)/5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f–1
Answer the following:
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 5
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
If f(x) = `(x - 1)/(x + 1), x ≠ - 1` Show that f(f(x)) = `- 1/x`, Provided x ≠ 0
Let f : R → R be defined by
f(x) = `{(3x; x > 2),(2x^2; 1 ≤ x ≤ 2), (4x; x < 1):}`
Then f(-2) + f(1) + f(3) is ______
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Let f and g be two functions given by f = {(2, 4), (5, 6), (8, – 1), (10, – 3)} g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, – 5)} then. Domain of f + g is ______.
Find the domain of the following functions given by f(x) = `1/sqrt(1 - cos x)`
Find the domain of the following function given by:
f(x) = `(3x)/(2x - 8)`
Find the range of the following functions given by f(x) = 1 + 3 cos2x
(Hint: –1 ≤ cos 2x ≤ 1 ⇒ –3 ≤ 3 cos 2x ≤ 3 ⇒ –2 ≤ 1 + 3cos 2x ≤ 4)
Domain of `sqrt(a^2 - x^2) (a > 0)` is ______.
The domain of the function f(x) = `1/sqrt(|x| - x)` is ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
