Advertisements
Advertisements
Question
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(0)
Solution
f(x) = x2 + 3, x ≤ 2
= 5x + 7, x > 2
f(0) = 02 + 3
= 3
APPEARS IN
RELATED QUESTIONS
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
If f(x) = x2, find \[\frac{f\left( 1 . 1 \right) - f\left( 1 \right)}{\left( 1 . 1 \right) - 1}\]
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
If f(x) = 4x − x2, x ∈ R, then write the value of f(a + 1) −f(a − 1).
The range of f(x) = cos [x], for π/2 < x < π/2 is
If f(x) = cos (log x), then value of \[f\left( x \right) f\left( 4 \right) - \frac{1}{2} \left\{ f\left( \frac{x}{4} \right) + f\left( 4x \right) \right\}\] is
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
Check if the following relation is function:
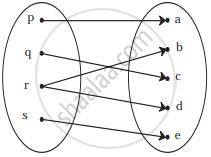
If f(m) = m2 − 3m + 1, find f(− x)
Find x, if f(x) = g(x) where f(x) = x4 + 2x2, g(x) = 11x2
Express the following logarithmic equation in exponential form
log10 (0.001) = −3
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f + g) (x)
Answer the following:
Show that, `log |sqrt(x^2 + 1) + x | + log | sqrt(x^2 + 1) - x|` = 0
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find the height of a person whose forehand length is 40 cm
The domain of the function f(x) = `sqrtx` is ______.
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
The range of the function f(x) = x2 + 2x+ 2 is ______.
