Advertisements
Advertisements
Question
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(2)
Solution
f(x) = x2 + 3, x ≤ 2
= 5x + 7, x > 2
f(2) = 22 + 3
= 4 + 3
= 7
APPEARS IN
RELATED QUESTIONS
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The domain of definition of the function f(x) = log |x| is
Find x, if g(x) = 0 where g(x) = x3 − 2x2 − 5x + 6
Find x, if f(x) = g(x) where f(x) = x4 + 2x2, g(x) = 11x2
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x3
Express the following exponential equation in logarithmic form
25 = 32
Express the following exponential equation in logarithmic form
10−2 = 0.01
Express the following logarithmic equation in exponential form
`log_(1/2) (8)` = – 3
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Find the range of the following function.
f(x) = 1 + 2x + 4x
A graph representing the function f(x) is given in it is clear that f(9) = 2
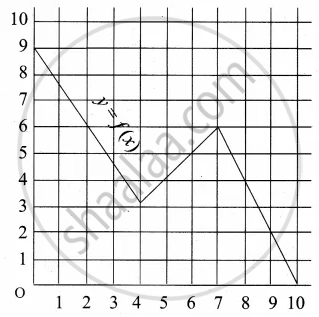
For what value of x is f(x) = 1?
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
Domain of function f(x) = cos–1 6x is ______.
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
The expression \[\begin{array}{cc}\log_p\log_p\sqrt[p]{\sqrt[p]{\sqrt[p]{\text{...........}\sqrt[p]{p}}}}\\
\phantom{...........}\ce{\underset{n radical signs}{\underline{\uparrow\phantom{........}\uparrow}}}
\end{array}\]where p ≥ 2, p ∈ N; ∈ N when simplified is ______.
