Advertisements
Advertisements
Question
Express the following exponential equation in logarithmic form
10−2 = 0.01
Solution
| Exponential form | Logarithmic form |
| 10−2 = 0.01 |
– 2 = log10 (0.01) |
APPEARS IN
RELATED QUESTIONS
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vii) f2 + 7f
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
Write the domain and range of \[f\left( x \right) = \sqrt{x - \left[ x \right]}\] .
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right)\] , then \[f\left( \frac{2x}{1 + x^2} \right)\] is equal to
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
The domain of definition of the function \[f\left( x \right) = \sqrt{x - 1} + \sqrt{3 - x}\] is
The range of the function f(x) = |x − 1| is
If f(m) = m2 − 3m + 1, find `f(1/2)`
If ƒ(m) = m2 − 3m + 1, find f(x + 1)
If f(m) = m2 − 3m + 1, find f(− x)
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Which of the following relations are functions? If it is a function determine its domain and range:
{(0, 0), (1, 1), (1, −1), (4, 2), (4, −2), (9, 3), (9, −3), (16, 4), (16, −4)}
Check if the following relation is a function.
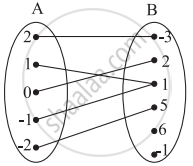
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 3), (4, 1), (2, 2)}
Find the domain and range of the following function.
f(x) = `sqrt(16 - x^2)`
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also find its domain
Let f be a subset of Z × Z defined by f = {(ab, a + b) : a, b ∈ Z}. Is f a function from Z to Z? Justify?
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Express the following exponential equation in logarithmic form
e–x = 6
Prove that logbm a = `1/"m" log_"b""a"`
Answer the following:
Find whether the following function is one-one
f : R − {3} → R defined by f(x) = `(5x + 7)/(x - 3)` for x ∈ R − {3}
Answer the following:
For any base show that log (1 + 2 + 3) = log 1 + log 2 + log 3
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
Find value of `(3 + log_10 343)/(2 + 1/2 log_10 (49/4) + 1/2 log_10 (1/25)`
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the domain of the following function.
f(x) = 5–xPx–1
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
Let A = {1, 2, 3, 4} and B = N. Let f : A → B be defined by f(x) = x3 then, find the range of f
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
If f(x) = 5x - 3, then f-1(x) is ______
Find the range of the following functions given by f(x) = 1 + 3 cos2x
(Hint: –1 ≤ cos 2x ≤ 1 ⇒ –3 ≤ 3 cos 2x ≤ 3 ⇒ –2 ≤ 1 + 3cos 2x ≤ 4)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
If f(x) = `log_e{((1 - x))/((1 - x))}, |x| < 1, f{(2x)/((1 + x^2))}` is equal to ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
