Advertisements
Advertisements
Question
Answer the following:
Find value of `(3 + log_10 343)/(2 + 1/2 log_10 (49/4) + 1/2 log_10 (1/25)`
Solution
`(3 + log_10 343)/(2 + 1/2 log_10 (49/4) + 1/2 log_10 (1/25)`
= `(3 + log_10 7^3)/(2 + log_10 (49/4)^(1/2) + log_10 (1/25)^(1/2)`
= `(3 + 3.log_10 7)/(2 + log_10 7/2 + log_10 1/5)`
= `(3(1 + log_10 7))/(2 + log_10 (7/2 xx 1/5)`
= `(3(1 + log_10 7))/(2 + log_10 (7/10))`
= `(3(1 + log_10 7))/(2 + log_10 7 - log_10 10)`
= `(3(1 + log_10 7))/(2 + log_10 7 - 1)` ...[∵ loga a = 1]
= `(3(1 + log_10 7))/(1 + log_10 7)`
= 3
APPEARS IN
RELATED QUESTIONS
If \[f\left( x \right) = \frac{x + 1}{x - 1}\] , show that f[f[(x)]] = x.
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
If for non-zero x, af(x) + bf \[\left( \frac{1}{x} \right) = \frac{1}{x} - 5\] , where a ≠ b, then find f(x).
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
If f(x) = cos (log x), then the value of f(x2) f(y2) −
If \[f\left( x \right) = \frac{\sin^4 x + \cos^2 x}{\sin^2 x + \cos^4 x}\] for x ∈ R, then f (2002) =
The domain of definition of the function \[f\left( x \right) = \sqrt{x - 1} + \sqrt{3 - x}\] is
The domain of definition of the function f(x) = log |x| is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
Let \[f\left( x \right) = \sqrt{x^2 + 1}\ ] . Then, which of the following is correct?
Check if the following relation is function:
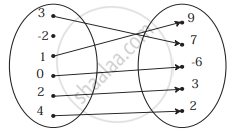
If f(m) = m2 − 3m + 1, find f(−3)
If f(m) = m2 − 3m + 1, find f(x + 1)
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x3
Express the following exponential equation in logarithmic form
25 = 32
Express the following logarithmic equation in exponential form
log2 64 = 6
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Find the domain of f(x) = ln (x − 5)
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
Write the following expression as a single logarithm.
`1/3 log (x - 1) + 1/2 log (x)`
Solve for x.
log2 + log(x + 3) – log(3x – 5) = log3
Answer the following:
If f(x) = 3x + a and f(1) = 7 find a and f(4)
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Check if this relation is a function
The domain of the function f(x) = `sqrtx` is ______.
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Find the range of the following functions given by f(x) = 1 + 3 cos2x
(Hint: –1 ≤ cos 2x ≤ 1 ⇒ –3 ≤ 3 cos 2x ≤ 3 ⇒ –2 ≤ 1 + 3cos 2x ≤ 4)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
The domain and range of real function f defined by f(x) = `sqrt(x - 1)` is given by ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
