Advertisements
Advertisements
Question
Express the following exponential equation in logarithmic form
e–x = 6
Solution
e–x = 6
∴ – x = loge 6 …[By definition of logarithm]
i.e. loge 6 = – x
APPEARS IN
RELATED QUESTIONS
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
find: f(1), f(−1), f(0) and f(2).
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(c) whether f(xy) = f(x) : f(y) holds
et A = (12, 13, 14, 15, 16, 17) and f : A → Z be a function given by
f(x) = highest prime factor of x.
Find range of f.
Let A = [p, q, r, s] and B = [1, 2, 3]. Which of the following relations from A to B is not a function?
If f(x) = (x − a)2 (x − b)2, find f(a + b).
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
Write the range of the function f(x) = ex−[x], x ∈ R.
If\[f\left( x \right) = 1 - \frac{1}{x}\] , then write the value of \[f\left( f\left( \frac{1}{x} \right) \right)\]
If f, g, h are real functions given by f(x) = x2, g(x) = tan x and h(x) = loge x, then write the value of (hogof)\[\left( \sqrt{\frac{\pi}{4}} \right)\] .
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
The range of f(x) = cos [x], for π/2 < x < π/2 is
Which of the following are functions?
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right)\] , then \[f\left( \frac{2x}{1 + x^2} \right)\] is equal to
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
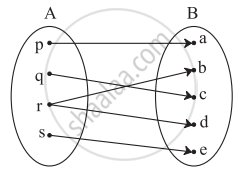
Check if the following relation is a function.
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
Check if the relation given by the equation represents y as function of x:
2y + 10 = 0
If f(m) = m2 − 3m + 1, find f(0)
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Express the following exponential equation in logarithmic form
25 = 32
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following logarithmic equation in exponential form
log10 (0.001) = −3
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
Solve for x.
2 log10 x = `1 + log_10 (x + 11/10)`
Select the correct answer from given alternatives.
If log (5x – 9) – log (x + 3) = log 2 then x = ...............
Select the correct answer from given alternatives.
If f : R → R is defined by f(x) = x3 then f–1 (8) is equal to :
Answer the following:
Find whether the following function is one-one
f : R − {3} → R defined by f(x) = `(5x + 7)/(x - 3)` for x ∈ R − {3}
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
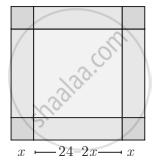
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Write an expression for gf(x) in its simplest form
Let f : R → R be defined by
f(x) = `{(3x; x > 2),(2x^2; 1 ≤ x ≤ 2), (4x; x < 1):}`
Then f(-2) + f(1) + f(3) is ______
Find the domain of the following function.
f(x) = [x] + x
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f – g)(x)
The expression \[\begin{array}{cc}\log_p\log_p\sqrt[p]{\sqrt[p]{\sqrt[p]{\text{...........}\sqrt[p]{p}}}}\\
\phantom{...........}\ce{\underset{n radical signs}{\underline{\uparrow\phantom{........}\uparrow}}}
\end{array}\]where p ≥ 2, p ∈ N; ∈ N when simplified is ______.
If f : R – {2} `rightarrow` R i s a function defined by f(x) = `(x^2 - 4)/(x - 2)`, then its range is ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
