Advertisements
Advertisements
Question
Let A = [p, q, r, s] and B = [1, 2, 3]. Which of the following relations from A to B is not a function?
Options
(a) R1 = [(p, 1), (q, 2), (r, 1), (s, 2)]
(b) R2 = [(p, 1), (q, 1), (r, 1), (s, 1)]
(c) R3 = [(p, 1), (q, 2), (p, 2), (s, 3)
(d) R4 = [(p, 2), (q, 3), (r, 2), (s, 2)].
Solution
(c) R3 = [(p, 1), (q, 2), (p, 2), (s, 3)
All the relations in (a), (b) and (d) have a unique image in B for all the elements in A.
R3 is not a function from A to B because p ∈ A has two images, 1 and 2, in B.
Hence, option (c) is not a function.
APPEARS IN
RELATED QUESTIONS
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
Define a function as a correspondence between two sets.
et A = (12, 13, 14, 15, 16, 17) and f : A → Z be a function given by
f(x) = highest prime factor of x.
Find range of f.
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
Write the domain and range of \[f\left( x \right) = \sqrt{x - \left[ x \right]}\] .
Let f : R → R be defined by f(x) = 2x + |x|. Then f(2x) + f(−x) − f(x) =
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
The range of the function f(x) = |x − 1| is
Let \[f\left( x \right) = \sqrt{x^2 + 1}\ ] . Then, which of the following is correct?
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(2)
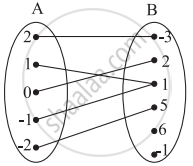
Check if the following relation is a function.
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
If f(m) = m2 − 3m + 1, find f(0)
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Find the domain and range of the follwoing function.
h(x) = `sqrt(x + 5)/(5 + x)`
Find the domain and range of the following function.
f(x) = `sqrt((x - 3)/(7 - x))`
Express the following exponential equation in logarithmic form
54° = 1
Express the following exponential equation in logarithmic form
231 = 23
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following exponential equation in logarithmic form
e–x = 6
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Prove that alogcb = blogca
If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)2 = 20xy
The equation logx2 16 + log2x 64 = 3 has,
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
Answer the following:
Find x, if x = 33log32
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
Find the domain of the following function.
f(x) = 5–xPx–1
Answer the following:
Find the range of the following function.
f(x) = [x] – x
A graph representing the function f(x) is given in it is clear that f(9) = 2
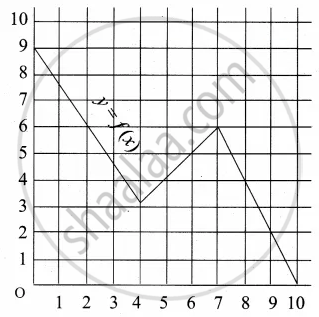
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
A function f is defined by f(x) = 2x – 3 find x such that f(x) = f(1 – x)
Find the domain of the function f given by f(x) = `1/sqrt([x]^2 - [x] - 6)`
If f(x) = `(x - 1)/(x + 1)`, then show that `f(- 1/x) = (-1)/(f(x))`
The domain of the function f(x) = `1/sqrt(|x| - x)` is ______.
