Advertisements
Advertisements
Question
A graph representing the function f(x) is given in it is clear that f(9) = 2
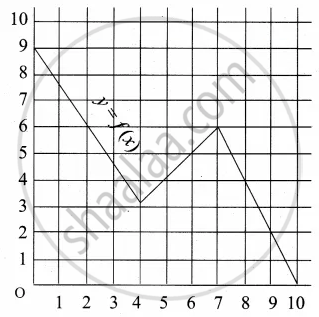
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
Solution
(a) f(0) = 9
(b) f(7) = 6
(c) f(2) = 6
(d) f(10) = 0
APPEARS IN
RELATED QUESTIONS
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
Let A = {1, 2, 3} and B = {2, 3, 4}. Then which of the following is a function from A to B?
Which of the following are functions?
If \[3f\left( x \right) + 5f\left( \frac{1}{x} \right) = \frac{1}{x} - 3\] for all non-zero x, then f(x) =
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
Express the following exponential equation in logarithmic form
10−2 = 0.01
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
