Advertisements
Advertisements
Question
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
Options
(a) {−1}
(b) {0}
(c) \[\left\{ - \frac{1}{2} \right\}\]
(d) ϕ
Solution
(c) \[\left\{ - \frac{1}{2} \right\}\]
Given:
\[f\left( x \right) = \begin{cases}- 1, & \text { for } - 2 \leq x \leq 0 \\ x - 1, &\text{ for } 0 \leq x \leq 2\end{cases}\]We know, \[\left| x \right| \geq 0\]
If \[x \leq 0\] , then \[\left| x \right| = - x\] ...(2)
APPEARS IN
RELATED QUESTIONS
What is the fundamental difference between a relation and a function? Is every relation a function?
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(i) f + g
Write the range of the function f(x) = ex−[x], x ∈ R.
Which of the following are functions?
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right) \text{ and} g\left( x \right) = \frac{3x + x^3}{1 + 3 x^2}\] , then f(g(x)) is equal to
If f(x) = cos (log x), then value of \[f\left( x \right) f\left( 4 \right) - \frac{1}{2} \left\{ f\left( \frac{x}{4} \right) + f\left( 4x \right) \right\}\] is
If \[f\left( x \right) = 64 x^3 + \frac{1}{x^3}\] and α, β are the roots of \[4x + \frac{1}{x} = 3\] . Then,
The domain of definition of the function \[f\left( x \right) = \sqrt{x - 1} + \sqrt{3 - x}\] is
If f(m) = m2 − 3m + 1, find f(0)
If f(m) = m2 − 3m + 1, find f(−3)
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(3)
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
If f(m) = m2 − 3m + 1, find f(0)
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
Express the following exponential equation in logarithmic form
231 = 23
Express the following logarithmic equation in exponential form
log10 (0.001) = −3
Answer the following:
Let f : R – {2} → R be defined by f(x) = `(x^2 - 4)/(x - 2)` and g : R → R be defined by g(x) = x + 2. Examine whether f = g or not
Answer the following:
Show that, `log |sqrt(x^2 + 1) + x | + log | sqrt(x^2 + 1) - x|` = 0
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
If `log"a"/(x + y - 2z) = log"b"/(y + z - 2x) = log"c"/(z + x - 2y)`, show that abc = 1
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
A function f is defined by f(x) = 2x – 3 find x such that f(x) = 0
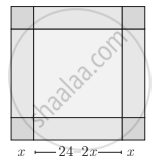
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
If f(x) = `(x - 1)/(x + 1), x ≠ - 1` Show that f(f(x)) = `- 1/x`, Provided x ≠ 0
The domain of the function f(x) = `sqrtx` is ______.
Find the domain of the following function given by:
f(x) = `(3x)/(2x - 8)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
