Advertisements
Advertisements
Question
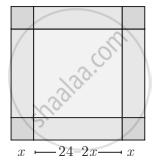
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
Solution
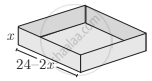
After cutting squares we will get a cuboid,
length of the cuboid (l) = 24 – 2x
breadth of the cuboid (b) = 24 – 2x
height of the cuboid (h) = 2x
Volume of the box = Volume of the cuboid
V = (24 – 2x)(24 – 2x) (x)
= (24 – 2x)2 (x)
= (576 + 4x2 – 96x) x
= 576x + 4x3 – 96x2
V = 4x3 – 96x2 + 576x
V(x) = 4x3 – 96x2 + 576x
APPEARS IN
RELATED QUESTIONS
Define a function as a correspondence between two sets.
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
Write the range of the real function f(x) = |x|.
If 2f (x) − \[3f\left( \frac{1}{x} \right) = x^2\] (x ≠ 0), then f(2) is equal to
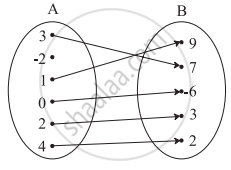
Check if the following relation is a function.
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Solve for x.
2 log10 x = `1 + log_10 (x + 11/10)`
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
