Advertisements
Advertisements
Question
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
Solution
(a) Given:
f (x) = x2 − 2x − 3
f (−2) = (− 2)2 − 2(− 2) − 3
= 4 + 4 – 3
= 8 − 3 = 5
f (−1) = (−1)2 − 2(−1) − 3
= 1+ 2 − 3
= 3 − 3 = 0
f (0) = (0)2 − 2(0) − 3
= 0 − 0 − 3
= − 3
f (1) = (1)2 − 2(1) − 3
= 1 − 2 − 3
=1 − 5 = − 4
f (2) = (2)2 – 2(2) − 3
= 4 − 4 – 3
= 4 – 7 = − 3
Thus, range of f(A) = (− 4, − 3, 0, 5).
APPEARS IN
RELATED QUESTIONS
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
If \[f\left( x \right) = \frac{x - 1}{x + 1}\] , then show that
(i) \[f\left( \frac{1}{x} \right) = - f\left( x \right)\]
(ii) \[f\left( - \frac{1}{x} \right) = - \frac{1}{f\left( x \right)}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iv) \[\frac{g}{f}\] Also, find (f + g) (−1), (fg) (0),
If f, g and h are real functions defined by
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
The range of f(x) = cos [x], for π/2 < x < π/2 is
The domain of definition of \[f\left( x \right) = \sqrt{4x - x^2}\] is
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Check if the following relation is a function.
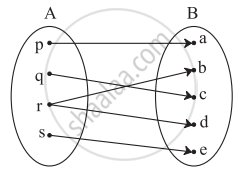
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
If f(m) = m2 − 3m + 1, find `f(1/2)`
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Find the domain and range of the following function.
f(x) = `sqrt((x - 2)(5 - x)`
Express the area A of circle as a function of its radius r
Express the following exponential equation in logarithmic form
e2 = 7.3890
Express the following exponential equation in logarithmic form
e–x = 6
Express the following logarithmic equation in exponential form
log2 64 = 6
Find the domain of f(x) = ln (x − 5)
If f(x) = 3x + 5, g(x) = 6x − 1, then find `("f"/"g") (x)` and its domain
The equation logx2 16 + log2x 64 = 3 has,
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Answer the following:
A function f : R → R defined by f(x) = `(3x)/5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f–1
Answer the following:
Let f : R → R be given by f(x) = x + 5 for all x ∈ R. Draw its graph
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
If f(x) = 5x - 3, then f-1(x) is ______
Let f : R → R be defined by
f(x) = `{(3x; x > 2),(2x^2; 1 ≤ x ≤ 2), (4x; x < 1):}`
Then f(-2) + f(1) + f(3) is ______
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
Find the domain of the following functions given by f(x) = `1/sqrt(1 - cos x)`
Find the range of the following functions given by f(x) = |x − 3|
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
Range of f(x) = `1/(1 - 2 cosx)` is ______.
Which of the following functions is NOT one-one?
Let f(θ) = sin θ (sin θ + sin 3θ) then ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
