Advertisements
Advertisements
Question
Express the area A of circle as a function of its radius r
Solution
If r is the radius of the circle, then area A is given by A = `pi"r"^2`
APPEARS IN
RELATED QUESTIONS
If f(x) = x2, find `(f(1.1) - f(1))/((1.1 - 1))`
find: f(1), f(−1), f(0) and f(2).
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(c) f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If \[f\left( x \right) = x^3 - \frac{1}{x^3}\] , show that
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
If f(x) = cos [π2]x + cos [−π2] x, where [x] denotes the greatest integer less than or equal to x, then write the value of f(π).
Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, −4), (4, 2), (5, 1)} and g = {(1, 0), (2, 2), (3, −1), (4, 4), (5, 3)}
Find the domain of fg.
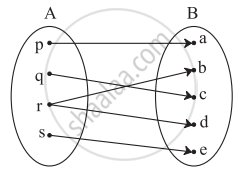
Which one of the following is not a function?
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
If \[f\left( x \right) = 64 x^3 + \frac{1}{x^3}\] and α, β are the roots of \[4x + \frac{1}{x} = 3\] . Then,
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
If \[\left[ x \right]^2 - 5\left[ x \right] + 6 = 0\], where [.] denotes the greatest integer function, then
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(0)
Check if the following relation is a function.
Find the domain and range of the following function.
f(x) = `sqrt((x - 2)(5 - x)`
Find the domain and range of the following function.
f(x) = `sqrt((x - 3)/(7 - x))`
Find the domain and range of the following function.
f(x) = `sqrt(16 - x^2)`
lf f(x) = 3(4x+1), find f(– 3)
Prove that `"b"^(log_"b""a"` = a
Solve for x.
2 log10 x = `1 + log_10 (x + 11/10)`
Select the correct answer from given alternatives.
Find x, if 2log2 x = 4
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Given the function f: x → x2 – 5x + 6, evaluate f(2)
A graph representing the function f(x) is given in it is clear that f(9) = 2
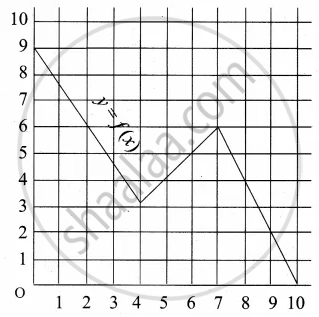
For what value of x is f(x) = 1?
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
If f(x) = `1/sqrt(4 - 3x)`, then dom(f) = ______..
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
The expression \[\begin{array}{cc}\log_p\log_p\sqrt[p]{\sqrt[p]{\sqrt[p]{\text{...........}\sqrt[p]{p}}}}\\
\phantom{...........}\ce{\underset{n radical signs}{\underline{\uparrow\phantom{........}\uparrow}}}
\end{array}\]where p ≥ 2, p ∈ N; ∈ N when simplified is ______.
