Advertisements
Advertisements
Question
Express the area A of circle as a function of its diameter d
Solution
Diameter (d) = 2r
∴ r = `"d"/2`
Area (A) = `pi"r"^2`
= `(pi"d"^2)/4`
APPEARS IN
RELATED QUESTIONS
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(b) {x : f(x) = −2}
et A = (12, 13, 14, 15, 16, 17) and f : A → Z be a function given by
f(x) = highest prime factor of x.
Find range of f.
If \[y = f\left( x \right) = \frac{ax - b}{bx - a}\] , show that x = f(y).
If for non-zero x, af(x) + bf \[\left( \frac{1}{x} \right) = \frac{1}{x} - 5\] , where a ≠ b, then find f(x).
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
If\[f\left( x \right) = 1 - \frac{1}{x}\] , then write the value of \[f\left( f\left( \frac{1}{x} \right) \right)\]
Let f and g be two functions given by
f = {(2, 4), (5, 6), (8, −1), (10, −3)} and g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, −5)}.
Find the domain of f + g
Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, −4), (4, 2), (5, 1)} and g = {(1, 0), (2, 2), (3, −1), (4, 4), (5, 3)}
Find the domain of fg.
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
If f(x) = sin [π2] x + sin [−π]2 x, where [x] denotes the greatest integer less than or equal to x, then
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
Let \[f\left( x \right) = \sqrt{x^2 + 1}\ ] . Then, which of the following is correct?
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
Find the domain and range of the following function.
g(x) = `(x + 4)/(x - 2)`
Find the domain and range of the following function.
f(x) = `root(3)(x + 1)`
Express the area A of a square as a function of its perimeter P
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Select the correct answer from given alternatives
The domain of `1/([x] - x)` where [x] is greatest integer function is
Answer the following:
Find x, if x = 33log32
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
If `log"a"/(x + y - 2z) = log"b"/(y + z - 2x) = log"c"/(z + x - 2y)`, show that abc = 1
Answer the following:
Find the domain of the following function.
f(x) = x!
Given the function f: x → x2 – 5x + 6, evaluate f(2a)
A graph representing the function f(x) is given in it is clear that f(9) = 2
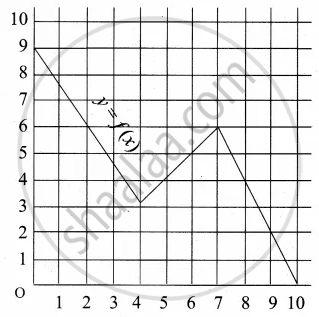
Describe the following Range
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
If f(x) = `(x - 1)/(x + 1)`, then show that `f(- 1/x) = (-1)/(f(x))`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
The domain and range of real function f defined by f(x) = `sqrt(x - 1)` is given by ______.
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
The range of the function y = `1/(2 - sin3x)` is ______.
The range of the function f(x) = x2 + 2x+ 2 is ______.
Let f(θ) = sin θ (sin θ + sin 3θ) then ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
