Advertisements
Advertisements
Question
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
Options
(a) [3/4, 1)
(b) (3/4, 1]
(c) [3/4, 1]
(d) (3/4, 1)
Solution
(c) [3/4, 1]
Given:
f(x) = cos2x + sin4x
\[\Rightarrow f\left( x \right) = 1 - \sin^2 x + \sin^4 x\]
\[\Rightarrow f\left( x \right) = \left( \sin^2 x - \frac{1}{2} \right)^2 + \frac{3}{4}\] The minimum value of \[f\left( x \right)\] is \[\frac{3}{4}\]
Also,
\[\sin^2 x \leq 1\]
\[ \Rightarrow \sin^2 x - \frac{1}{2} \leq \frac{1}{2}\]
\[ \Rightarrow \left( \sin^2 x - \frac{1}{2} \right)^2 \leq \frac{1}{4}\]
\[ \Rightarrow \left( \sin^2 x - \frac{1}{2} \right)^2 + \frac{3}{4} \leq \frac{1}{4} + \frac{3}{4}\]
\[ \Rightarrow f\left( x \right) \leq 1\]
The maximum value of
\[f\left( x \right)\] is 1.
∴ f(R) = (3/4, 1)
APPEARS IN
RELATED QUESTIONS
What is the fundamental difference between a relation and a function? Is every relation a function?
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(b) f2 = {(1, 1), (2, 7), (3, 5)}
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vii) f2 + 7f
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
Write the range of the function f(x) = ex−[x], x ∈ R.
If f, g, h are real functions given by f(x) = x2, g(x) = tan x and h(x) = loge x, then write the value of (hogof)\[\left( \sqrt{\frac{\pi}{4}} \right)\] .
The range of the function \[f\left( x \right) = \frac{x^2 - x}{x^2 + 2x}\] is
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
The domain of the function
The domain of definition of \[f\left( x \right) = \sqrt{4x - x^2}\] is
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Express the area A of a square as a function of its perimeter P
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Check the injectivity and surjectivity of the following function.
f : R → R given by f(x) = x2
Write the following expression as sum or difference of logarithm
`log (sqrt(x) root(3)(y))`
Write the following expression as sum or difference of logarithm
In `(("a"^3 ("a" - 2)^2)/sqrt("b"^2 + 5))`
If `log((x + y)/3) = 1/2 log x + 1/2 logy`, show that `x/y + y/x` = 7
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
A graph representing the function f(x) is given in it is clear that f(9) = 2
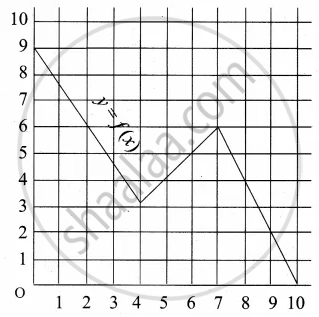
For what value of x is f(x) = 1?
A graph representing the function f(x) is given in it is clear that f(9) = 2
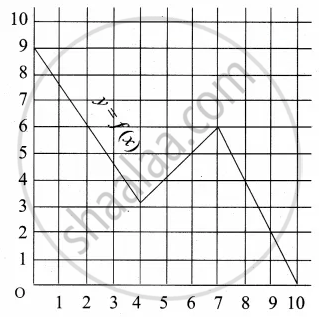
Describe the following Domain
A graph representing the function f(x) is given in it is clear that f(9) = 2
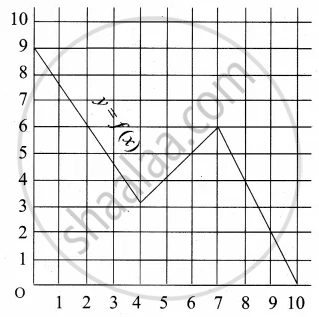
Describe the following Range
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
If f(x) = 5x - 3, then f-1(x) is ______
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
Find the domain of the following function.
f(x) = [x] + x
Find the range of the following functions given by f(x) = 1 + 3 cos2x
(Hint: –1 ≤ cos 2x ≤ 1 ⇒ –3 ≤ 3 cos 2x ≤ 3 ⇒ –2 ≤ 1 + 3cos 2x ≤ 4)
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
If f(x) = y = `(ax - b)/(cx - a)`, then prove that f(y) = x.
The domain of the function f given by f(x) = `(x^2 + 2x + 1)/(x^2 - x - 6)` is ______.
The range of the function y = `1/(2 - sin3x)` is ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
